题目内容
17.甲、乙两名同学做“石头、剪子、布”的游戏,随机出手一次,则甲获胜的概率是$\frac{1}{3}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与甲获胜的情况数,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有9种等可能的结果,甲获胜的情况数是3种,
∴一次游戏中甲获胜的概率是:$\frac{3}{9}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题主要考查了列表法和树状图法求概率知识,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
7.零上13℃记作+13℃,零下5℃记作( )
| A. | 5 | B. | -5 | C. | 5℃ | D. | -5℃ |
5.已知①线段,②平行四边形;③矩形;④等腰三角形;⑤圆;⑥菱形;⑦正六边形,其中既是轴对称又是中心对称图形的有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
12.已知反比例函数y=$\frac{k-1}{x}$图象的两个分支分别位于第二、四象限,则k的取值范围是( )
| A. | k>1 | B. | k<1 | C. | k>0 | D. | k<0 |
2.如图是按一定规律用若干个“○”排成的“龟图”,若第n个“龟图”中有245个“○”,则n=( )


| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
2. 如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=$\sqrt{2}$,则图中阴影部分的面积为( )
如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=$\sqrt{2}$,则图中阴影部分的面积为( )
 如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=$\sqrt{2}$,则图中阴影部分的面积为( )
如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=$\sqrt{2}$,则图中阴影部分的面积为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
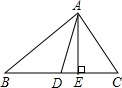 已知,如图,AD为△ABC的中线,且BD=4,若△ABC的面积为12,则高AE的长度为3.
已知,如图,AD为△ABC的中线,且BD=4,若△ABC的面积为12,则高AE的长度为3.


