题目内容
20.已知关于x的方程x2-2(m+1)x+m2-3=0(1)当m取何值时,方程有两个实数根?
(2)设x1、x2是方程的两根,且(x1-x2)2-x1x2=26,求m的值.
分析 (1)根据一元二次方程根的判别式的意义得到4(m+1)2-4(m2-3)≥0,然后解不等式即可;
(2)根据根与系数的关系得x1+x2=2(m+1),x1x2=m2-3,代入(x1-x2)2-x1x2=26,计算即可求解.
解答 解:(1)根据题意得△=4(m+1)2-4(m2-3)≥0,
解得m≥-2;
(2)当m≥-2时,x1+x2=2(m+1),x1x2=m2-3.
则(x1-x2)2-x1x2=(x1+x2)2-5x1x2=[2(m+1)]2-5(m2-3)=26,
即m2-8m+7=0,
解得m1=1>-2,m2=7>-2,
所以m1=1,m2=7.
点评 本题主要考查了一元二次方程根与系数的关系,一元二次方程根的判别式.
一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
5.据报道,三峡工程自兴建以来,累计发电量已突破8000亿千瓦时,若将8000亿用科学记数法表示8×10n,则n等于( )
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
10.已知x+$\frac{1}{x}$=3,则$\sqrt{x}$+$\frac{1}{\sqrt{x}}$的值为( )
| A. | -$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | ±$\sqrt{5}$ |
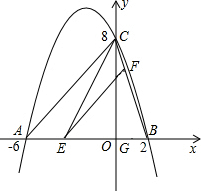 已知:抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
已知:抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.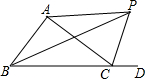 如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,连接AP,CP,若∠APC=65°,则∠ABC=50°.
如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,连接AP,CP,若∠APC=65°,则∠ABC=50°.