题目内容
15.已知实数a、b、c满足$|{a-\sqrt{8}}|+{({b-2})^2}+\sqrt{c-2\sqrt{3}}=0$,问以a、b、c为边能否构成三角形,若能请判别是什么三角形;若不能,请说明理由.分析 根据非负数的性质可求出a、b、c的值,首先根据三角形的三边关系判断能否构成三角形,利用勾股定理的逆定理证明三角形是直角三角形,
解答 解:根据题意得:a-$\sqrt{8}$=0,b-2=0,c-2$\sqrt{3}$=0,
解得:a=2$\sqrt{2}$,b=2,c=2$\sqrt{3}$,
∵a-b<c<a+b,
∴以a、b、c为边能构成三角形,
∵(2$\sqrt{2}$)2+(2)2=(2$\sqrt{3}$)2,
∴a2+b2=c2,
∴以a、b、c为边的三角形是直角三角形.
点评 本题考查了非负数的性质和勾股定理的逆定理,本题中证明三角形是直角三角形是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.某校组织了“讲文明、守秩序、迎南博”知识竞赛活动,从中抽取了7名同学的参赛成绩如下(单位:分):80,90,70,100,60,80,80.则这组数据的中位数和众数分别是( )
| A. | 90,80 | B. | 70,80 | C. | 80,80 | D. | 100,80 |
5.抛物线y=x2+2x-1的顶点坐标是( )
| A. | (1,2) | B. | (-1,-2) | C. | (1,-2) | D. | (-1,2) |
 己知,如图,矩形ABCD中,AD=3,DC=4,矩形EFGH的三个顶点E.G、H分别在矩形ABCD的边ABCD的边AB、CD、DA上,AH=1,连接CF.
己知,如图,矩形ABCD中,AD=3,DC=4,矩形EFGH的三个顶点E.G、H分别在矩形ABCD的边ABCD的边AB、CD、DA上,AH=1,连接CF.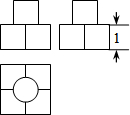 如图是某几何体的三视图,其中主视图和左视图是由若干个大小相等的正方形构成的.根据图中所标的尺寸,该几何体的表面积是16+π(不取近似值).
如图是某几何体的三视图,其中主视图和左视图是由若干个大小相等的正方形构成的.根据图中所标的尺寸,该几何体的表面积是16+π(不取近似值).


