题目内容
 如图,在四边形ABCD中,∠A-∠B=∠C-∠D,求证:AB∥CD.
如图,在四边形ABCD中,∠A-∠B=∠C-∠D,求证:AB∥CD.考点:平行线的判定,多边形内角与外角
专题:证明题
分析:由四边形内角和为360°结合条件可求得∠A+∠D=180°,可证明AB∥CD.
解答:证明:
∵∠A-∠B=∠C-∠D,
∴∠A+∠D=∠B+∠C,
又∠A+∠D+∠B+∠C=360°,
∴2(∠A+∠D)=360°,
∴∠A+∠D=180°,
∴AB∥CD.
∵∠A-∠B=∠C-∠D,
∴∠A+∠D=∠B+∠C,
又∠A+∠D+∠B+∠C=360°,
∴2(∠A+∠D)=360°,
∴∠A+∠D=180°,
∴AB∥CD.
点评:本题主要考查平行线的判定,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
小明的爸爸买了利率为3.96%的3年期债券,到期后可获得本息1678元,则小明的爸爸买债券花了( )
| A、1500元 |
| B、1600元 |
| C、1700元 |
| D、1800元 |
 如图,已知AB∥CE,证明:∠A+∠B+∠ACB=180°.
如图,已知AB∥CE,证明:∠A+∠B+∠ACB=180°. 如图,在△ABC中,AB的垂直平分线交AB于E,交BC于D,连结AD.若AC=4cm,△ADC的周长为11cm,则BC的长为
如图,在△ABC中,AB的垂直平分线交AB于E,交BC于D,连结AD.若AC=4cm,△ADC的周长为11cm,则BC的长为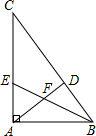 在△ABC中,∠CAB=90°,AD⊥BC于D,BE平分∠CBA交AC于E,交AD于F,求证:AE=AF.
在△ABC中,∠CAB=90°,AD⊥BC于D,BE平分∠CBA交AC于E,交AD于F,求证:AE=AF.