题目内容
14.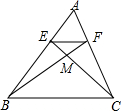 如图所示,△ABC中,EF∥BC,EC和FB相交于M,S△MEF:S△MBC=4:25,求AE:BE的值.
如图所示,△ABC中,EF∥BC,EC和FB相交于M,S△MEF:S△MBC=4:25,求AE:BE的值.
分析 根据EF∥BC,得到△EFM∽△BCM,由相似三角形的性质得到S△MEF:S△MBC=($\frac{EF}{BC}$)2=4:25,于是得到$\frac{EF}{BC}$=$\frac{2}{5}$,由于EF∥BC,推出△AEF∽△ABC,于是得到$\frac{AE}{AB}=\frac{EF}{BC}$=$\frac{2}{5}$,即可得到结论.
解答 解:∵EF∥BC,
∴△EFM∽△BCM,
∴S△MEF:S△MBC=($\frac{EF}{BC}$)2=4:25,
∴$\frac{EF}{BC}$=$\frac{2}{5}$,
∵EF∥BC,
∴△AEF∽△ABC,
∴$\frac{AE}{AB}=\frac{EF}{BC}$=$\frac{2}{5}$,
∴AE:BE=2:3.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
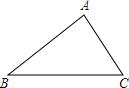 如图,在锐角三角形ABC中,AB=10,AC=2$\sqrt{13}$,sinB=$\frac{3}{5}$.
如图,在锐角三角形ABC中,AB=10,AC=2$\sqrt{13}$,sinB=$\frac{3}{5}$.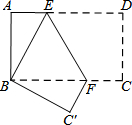 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.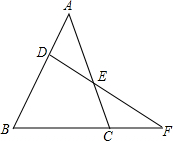 已知:如图△ABC中,D,E分别是AB,AC上的点,DE,BC的延长线相交于F,AD=CF,求证:$\frac{BC}{AB}$=$\frac{DE}{EF}$.
已知:如图△ABC中,D,E分别是AB,AC上的点,DE,BC的延长线相交于F,AD=CF,求证:$\frac{BC}{AB}$=$\frac{DE}{EF}$. 如图,已知AB:AD=AD:AE=BC:DE,试说明AD•CE=BD•AE.
如图,已知AB:AD=AD:AE=BC:DE,试说明AD•CE=BD•AE.