题目内容
4.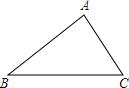 如图,在锐角三角形ABC中,AB=10,AC=2$\sqrt{13}$,sinB=$\frac{3}{5}$.
如图,在锐角三角形ABC中,AB=10,AC=2$\sqrt{13}$,sinB=$\frac{3}{5}$.(1)求tanC;
(2)求线段BC的长.
分析 (1)过点A作AD⊥BC于D,根据已知条件可得出AD,再利用勾股定理得出CD,进而得出tanC;
(2)在Rt△ABD中,利用勾股定理求出BD=8,结合CD的长度,即可得出BC的长.
解答 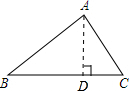 解:(1)如图,过点A作AD⊥BC于D,
解:(1)如图,过点A作AD⊥BC于D,
在Rt△ABD中,AB=10,sinB=$\frac{AD}{AB}$=$\frac{3}{5}$,
∴$\frac{AD}{10}$=$\frac{3}{5}$,
∴AD=6,
在Rt△ACD中,由勾股定理得CD2=AC2-AD2,
∴CD2=(2$\sqrt{13}$)2-62=16,
∴CD=4,
∴tanC=$\frac{AD}{CD}$=$\frac{6}{4}$=$\frac{3}{2}$;
(2)在Rt△ABD中,AB=10,AD=6,
∴由勾股定理得BD=8,
由(1)得CD=4,
∴BC=BD+CD=12.
点评 本题考查了解直角三角形以及勾股定理,要熟练掌握好边角之间的关系.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
15.若a=-2×52,b=-(2×5)2,c=-(2-5)2,则a、b、c的大小关系是( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | b<c<a |
12.下列各数中,最小的数为( )
| A. | 2 | B. | -3 | C. | 0 | D. | -2 |

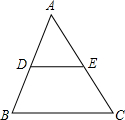 如图所示,在△ABC中,DE∥BC,若AD=1,DB=2,则$\frac{{S}_{△ADE}}{{S}_{四边形BCED}}$=$\frac{1}{8}$.
如图所示,在△ABC中,DE∥BC,若AD=1,DB=2,则$\frac{{S}_{△ADE}}{{S}_{四边形BCED}}$=$\frac{1}{8}$. 如图,已知四边形ABCD是平行四边形,AC为对角线,∠DAC=30°,∠ACD=90°,AD=8,点M为AC的中点,动点E从点C出发以每秒1个单位的速度运动到点B停止,连接EM并延长交AD于点F,设点E的运动时间为t秒.
如图,已知四边形ABCD是平行四边形,AC为对角线,∠DAC=30°,∠ACD=90°,AD=8,点M为AC的中点,动点E从点C出发以每秒1个单位的速度运动到点B停止,连接EM并延长交AD于点F,设点E的运动时间为t秒.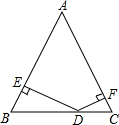 [问题提出]
[问题提出]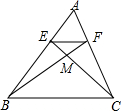 如图所示,△ABC中,EF∥BC,EC和FB相交于M,S△MEF:S△MBC=4:25,求AE:BE的值.
如图所示,△ABC中,EF∥BC,EC和FB相交于M,S△MEF:S△MBC=4:25,求AE:BE的值.