题目内容
2.解方程①$\frac{6}{(x+1)(x-2)}-\frac{2}{x-2}=1$;
②3x(x+2)=5(x+2)
分析 ①先把分式方程转化为整式方程,再根据解整式方程的步骤求出x的值,然后进行检验,即可得出答案;
②先把等号右边的式子移到左边,再提取公因式,然后求解即可.
解答 解:①$\frac{6}{(x+1)(x-2)}$-$\frac{2}{x-2}$=1,
去分母得:6-2(x+1)=(x+1)(x-2),
去括号得:6-2x-2=x2-x-2,
合并同类项得:x2+x-6=0,
整理得:(x+3)(x-2)=0,
解得:x1=-3,x2=2,
经检验x1=-3是原方程的解,x2=2不是原方程的解,
则原方程的解是x=-3;
②3x(x+2)=5(x+2),
3x(x+2)-5(x+2)=0,
(x+2)(3x-5)=0,
x+2=0或3x-5=0,
x1=-2,x2=$\frac{5}{3}$.
点评 此题考查了分式方程的解和因式分解法解一元二次方程,解分式方程的基本思想是把分式方程转化为整式方程.具体方法是方程两边同时乘以最简公分母,在此过程中有可能会产生增根,增根是转化后整式的根,不是原方程的根;因式分解法解一元二次方程时,有公因式的一定先提取公因式.

练习册系列答案
相关题目
12.下列各数中,最小的数为( )
| A. | 2 | B. | -3 | C. | 0 | D. | -2 |
 [问题提出]
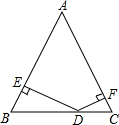
[问题提出] 如图,在△ABC中,∠1=∠A,若BD=2,AD=3,则BC=$\sqrt{10}$.
如图,在△ABC中,∠1=∠A,若BD=2,AD=3,则BC=$\sqrt{10}$.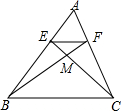 如图所示,△ABC中,EF∥BC,EC和FB相交于M,S△MEF:S△MBC=4:25,求AE:BE的值.
如图所示,△ABC中,EF∥BC,EC和FB相交于M,S△MEF:S△MBC=4:25,求AE:BE的值.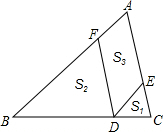 如图,D为△ABC的边BC上的一点,DE∥AB,DF∥AC,分别交AC,AB于点E,F,设△CDE,△BDF,四边形DEAF的面积分别为S1,S2,S3,求证:S3=2$\sqrt{{S}_{1}{S}_{2}}$.
如图,D为△ABC的边BC上的一点,DE∥AB,DF∥AC,分别交AC,AB于点E,F,设△CDE,△BDF,四边形DEAF的面积分别为S1,S2,S3,求证:S3=2$\sqrt{{S}_{1}{S}_{2}}$.