题目内容
9.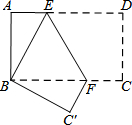 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.(1)△BEF是等腰三角形吗?试说明理由;
(2)若AB=8,DE=10,求CF的长度.
分析 (1)由翻折的性质得∠DEF=∠BEF,由长方形纸片的上下两边平行,可得∠DEF=∠BFE,所以∠BEF=∠BFE,根据“等角对等边”可知△BEF是等腰三角形;
(2)由翻折的性质可知BE=ED=10,由勾股定理可求得AE=6,从而得到AD=16,然后根据EB=FB=10可求得FC=6.
解答 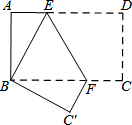 解:(1)如图,由翻折的性质得:∠DEF=∠BEF,
解:(1)如图,由翻折的性质得:∠DEF=∠BEF,
∵四边形ABCD为矩形,
∴AD∥BC.
∴∠DEF=∠BFE.
∴∠BEF=∠BFE.
∴BE=BF.
∴△BEF是等腰三角形.
(2)由翻折的性质可知BE=ED=10,
在Rt△ABE中,由勾股定理得:AE=$\sqrt{B{E}^{2}-A{B}^{2}}$=6.
∴AD=AE+ED=6+10=16.
∴BC=16.
由(1)可知:BF=BE=10,
∴FC=BC-BF=16-10=6.
∴FC=6.
点评 本题主要考查的是翻折的性质、矩形的性质、等腰三角形的判定、勾股定理的应用,证得BF=BE是解题的关键.

练习册系列答案
相关题目
20.下列图象中,表示直线y=-x+1的是( )
| A. |  | B. |  | C. |  | D. |  |
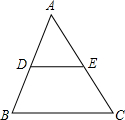 如图所示,在△ABC中,DE∥BC,若AD=1,DB=2,则$\frac{{S}_{△ADE}}{{S}_{四边形BCED}}$=$\frac{1}{8}$.
如图所示,在△ABC中,DE∥BC,若AD=1,DB=2,则$\frac{{S}_{△ADE}}{{S}_{四边形BCED}}$=$\frac{1}{8}$.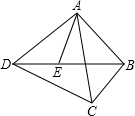 E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.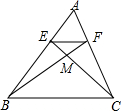 如图所示,△ABC中,EF∥BC,EC和FB相交于M,S△MEF:S△MBC=4:25,求AE:BE的值.
如图所示,△ABC中,EF∥BC,EC和FB相交于M,S△MEF:S△MBC=4:25,求AE:BE的值. 如图,已知D为△ABC的内心,∠A=m,∠D=n,请你探究m、n之间的关系,并证明你的结论.
如图,已知D为△ABC的内心,∠A=m,∠D=n,请你探究m、n之间的关系,并证明你的结论.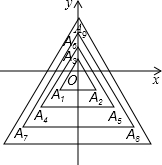 如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们
如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们