题目内容
12. 如图,直线l1与直线l2:y=$\frac{3}{4}$x相交于点A(2a+1,3),且与y轴交于点B(0,6).
如图,直线l1与直线l2:y=$\frac{3}{4}$x相交于点A(2a+1,3),且与y轴交于点B(0,6).(1)求a的值;
(2)求直线11的函数关系式;
(3)直线l平行于y轴,分别交直线l1,l2、x轴于点M、N、P,设点P的横坐标为t(t>0,t≠4),在y轴上是否存在点F,使得△FMN为等腰直角三角形?若存在,请求出t的值;若不存在,请说明理由.
分析 (1)把点A(2a+1,3)代入y=$\frac{3}{4}$x,即可求得a的值;
(2)利用待定系数法即可求得直线11的函数关系式;
(3)分别利用t表示出M、N的坐标,可表示出MN,分∠FMN、∠FNM和∠MFN为直角三种情况,分别求得F点的坐标,表示出FM、FN,分别得到关于m的方程可求得m.
解答 解:(1)∵直线l2:y=$\frac{3}{4}$x经过点A(2a+1,3),
∴3=$\frac{3}{4}$(2a+1),
解得a=$\frac{3}{2}$;
(2)设直线11的函数关系式y=kx+b,
∵点A(4,3),点B(0,6).
∴$\left\{\begin{array}{l}{4k+b=3}\\{b=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=6}\end{array}\right.$.
∴直线11的函数关系式y=-$\frac{3}{4}$x+6;
(3)∵P(t,0)(t>0,t≠4),则M(t,-$\frac{3}{4}$t+6),N(t,$\frac{3}{4}$t),
∴MN=|-$\frac{3}{2}$t+6|,
Ⅰ)当∠FMN=90°且△FMN为等腰三角形时,F(0,-$\frac{3}{4}$t+6),
∴FM=MN,即:t=|-$\frac{3}{2}$t+6|,
解得:t=$\frac{12}{5}$或t=12,
Ⅱ)同理当∠FNM=90°且△FMN为等腰三角形时,F(0,$\frac{3}{4}$t),
∴FN=MN,即:t=|-$\frac{3}{2}$t+6|,
解得:t=$\frac{12}{5}$或t=12,
Ⅲ)当∠MFN=90°且△FMN为等腰三角形时,F(0,3),
∴FM2=t2+($\frac{3}{4}$t-3)2,
FN2=t2+($\frac{3}{4}$t-3)2,
MN2=(-$\frac{3}{2}$t+6)2,
∴MN2=FM2+FN2,
∴t2+($\frac{3}{4}$t-3)2+t2+($\frac{3}{4}$t-3)2=(-$\frac{3}{2}$t+6)2,整理可得$\frac{7}{8}$t2+18t-18=0,解得t=$\frac{12}{7}$或t=-12(舍去);
综上可知存在使得△FMN为等腰直角三角形的点F,此时t的值为$\frac{12}{5}$或$\frac{12}{7}$或12.
点评 本题主要考查待定系数法求函数解析式和等腰三角形的判定、勾股定理等知识点的综合应用.掌握等腰三角形的判定和性质是解题的关键,在(3)中利用t表示出FN、FM和MN得到关于t的方程是解题的关键,注意分类讨论思想和方程思想的应用.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
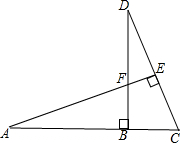 如图所示,点A,B,C在同一条直线上,BD⊥AC于B,AE⊥DC于E,BF=BC,求证:AF=DC.
如图所示,点A,B,C在同一条直线上,BD⊥AC于B,AE⊥DC于E,BF=BC,求证:AF=DC.