题目内容
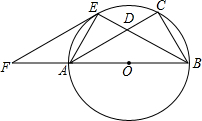 已知:如图,以Rt△ABC的边AB为直径作△ABC的外接圆O,∠B的平分线BE交AC于D,交⊙O于E,作EF∥AC交BA的延长线于F.
已知:如图,以Rt△ABC的边AB为直径作△ABC的外接圆O,∠B的平分线BE交AC于D,交⊙O于E,作EF∥AC交BA的延长线于F.(1)求证:EF是⊙O的切线;
(2)求证:AE2=CD•EF;
(3)若AB=15,EF=10,求DC的长.
考点:切线的判定,相似三角形的判定与性质
专题:
分析:(1)要证EF是⊙O的切线,只要连接OE,再证∠FEO=90°即可;
(2)连接CE,可证明△FEA∽△ECD,得出
=
,即AE•EC=CD•EF,再由AE=CE,即可得出AE2=CD•EF;
(3)证明△FEA∽△FBA,得出AE,BF的比例关系式,勾股定理得出AE,BF的关系式,求出AE的长,即可得出CD的长.
(2)连接CE,可证明△FEA∽△ECD,得出
| EF |
| EC |
| EA |
| CD |
(3)证明△FEA∽△FBA,得出AE,BF的比例关系式,勾股定理得出AE,BF的关系式,求出AE的长,即可得出CD的长.
解答: 解:(1)证明:连接OE,
解:(1)证明:连接OE,
∵∠B的平分线BE交AC于D,
∴∠CBE=∠ABE.
∵EF∥AC,
∴∠CAE=∠FEA.
∵∠OBE=∠OEB,∠CBE=∠CAE,
∴∠FEA=∠OEB.
∵∠AEB=90°,
∴∠FEO=90°.
∴OE⊥EF,
∴EF是⊙O切线.
(2)连接CE,
∵∠B的平分线BE交AC于D,
∴AE=CE,
∵EF∥AC,
∴∠F=∠BAC,
∵∠FEA=∠OEB,∠OBE=∠ACE,
∴∠FEA=∠ECA,
∴△FEA∽△ECD,
∴
=
,
即AE•EC=CD•EF,
∴AE2=CD•EF;
(3)∵∠FEA=∠OEB,∠OBE=∠OEB,
∴∠FEA=∠EBA,
∴△AEF∽△EBF,
∴AE:BE=EF:BF=1:2,
∴AF•FB=EF•EF,
∴AF(AF+15)=10×10.
∴AF=5.
∴FB=20.
∵EF=10
∵AE2+BE2=152,
∴AE=3
,
∴DC=
=4.5.
 解:(1)证明:连接OE,
解:(1)证明:连接OE,∵∠B的平分线BE交AC于D,
∴∠CBE=∠ABE.
∵EF∥AC,
∴∠CAE=∠FEA.
∵∠OBE=∠OEB,∠CBE=∠CAE,
∴∠FEA=∠OEB.
∵∠AEB=90°,
∴∠FEO=90°.
∴OE⊥EF,
∴EF是⊙O切线.
(2)连接CE,
∵∠B的平分线BE交AC于D,
∴AE=CE,
∵EF∥AC,
∴∠F=∠BAC,
∵∠FEA=∠OEB,∠OBE=∠ACE,
∴∠FEA=∠ECA,
∴△FEA∽△ECD,
∴
| EF |
| EC |
| EA |
| CD |
即AE•EC=CD•EF,
∴AE2=CD•EF;
(3)∵∠FEA=∠OEB,∠OBE=∠OEB,
∴∠FEA=∠EBA,
∴△AEF∽△EBF,
∴AE:BE=EF:BF=1:2,
∴AF•FB=EF•EF,
∴AF(AF+15)=10×10.
∴AF=5.
∴FB=20.
∵EF=10
∵AE2+BE2=152,
∴AE=3
| 5 |
∴DC=
| AE2 |
| EF |
点评:本题考查了切线的判定以及相似三角形的判定和性质,要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
 如图,已知AB∥CD,∠1=110°,则∠A的度数是( )
如图,已知AB∥CD,∠1=110°,则∠A的度数是( )| A、70° | B、100° |
| C、110° | D、130° |
2014年一季度,全国新增就业人数为416万人,用科学记数法表示416万正确的是( )人.
| A、4.16×107 |
| B、4.16×106 |
| C、4.16×105 |
| D、4.16×104 |
 如图,二次函数y=ax2+bx+c图象的对称轴为直线x=-1,与x轴交于点(1,0)和(m,0),与y轴交于负半轴.则下列结论:
如图,二次函数y=ax2+bx+c图象的对称轴为直线x=-1,与x轴交于点(1,0)和(m,0),与y轴交于负半轴.则下列结论: 如图,A,B两点分别位于一个池塘的两端,完成下图并求出A、B的距离.
如图,A,B两点分别位于一个池塘的两端,完成下图并求出A、B的距离. 如图,平行四边形ABCD中,E是AB的中点,G是CD上任意一点,平行四边形ABCD的面积为1,求△BEG的面积.
如图,平行四边形ABCD中,E是AB的中点,G是CD上任意一点,平行四边形ABCD的面积为1,求△BEG的面积. 如图,△ABC中,AB=AC,AD=AE=EB,BC=BE,求∠A的度数.
如图,△ABC中,AB=AC,AD=AE=EB,BC=BE,求∠A的度数.