题目内容
 如图,二次函数y=ax2+bx+c图象的对称轴为直线x=-1,与x轴交于点(1,0)和(m,0),与y轴交于负半轴.则下列结论:
如图,二次函数y=ax2+bx+c图象的对称轴为直线x=-1,与x轴交于点(1,0)和(m,0),与y轴交于负半轴.则下列结论:①m=-3,②abc<0,③4a-2b+c<0,④当x<1时,y<0,⑤8a+c>0.
其中正确结论的个数是( )
| A、5个 | B、4个 | C、3个 | D、2个 |
考点:二次函数图象与系数的关系
专题:数形结合
分析:根据抛物线的对称性得到抛物线与x轴的交点坐标为(-3,0)和(1,0),则m=-3,且观察函数图象得到当-3<x<1时,y<0,于是可对①④进行判断;
由抛物线开口方向得a>0,由抛物线的对称轴为直线x=-
=-1得到b=2a,则b>0,由抛物线与y轴的交点位置得c<0,所以abc<0,于是可对②进行判断;由于x=-2时,函数值小于0,则4a-2b+c<0,于是可对③进行判断;由于当x=2时,y>0,则4a+2b+c<0,然后把b=2a代入得到8a+c>0,于是可对⑤进行判断.
由抛物线开口方向得a>0,由抛物线的对称轴为直线x=-
| b |
| 2a |
解答:解:∵对称轴为直线x=-1,
∴点(1,0)和(m,0)关于直线x=-1对称,
∴m=-3,所以①正确;
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=-
=-1,
∴b=2a,
∴b>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以②正确;
∵当x=-2时,y<0,
∴4a-2b+c<0,所以③正确;
∵抛物线与x轴的交点坐标为(-3,0)和(1,0),
∴当-3<x<1时,y<0,所以④错误;
∵当x=2时,y>0,
∴4a+2b+c<0,
而b=2a,
∴4a+4a+c>0,即8a+c>0,所以⑤正确.
故选B.
∴点(1,0)和(m,0)关于直线x=-1对称,
∴m=-3,所以①正确;
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=-
| b |
| 2a |
∴b=2a,
∴b>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以②正确;
∵当x=-2时,y<0,
∴4a-2b+c<0,所以③正确;
∵抛物线与x轴的交点坐标为(-3,0)和(1,0),
∴当-3<x<1时,y<0,所以④错误;
∵当x=2时,y>0,
∴4a+2b+c<0,
而b=2a,
∴4a+4a+c>0,即8a+c>0,所以⑤正确.
故选B.
点评:本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);△决定抛物线与x轴交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )
如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )| A、90° | B、100° |
| C、110° | D、120° |
 如图几何体的主视图是( )
如图几何体的主视图是( )A、 |
B、 |
C、 |
D、 |
 如图,长方形ABCD中放置了9个形状、大小都相同的小长方形,求图中阴影部分的面积( )
如图,长方形ABCD中放置了9个形状、大小都相同的小长方形,求图中阴影部分的面积( )| A、72 | B、82 | C、65 | D、85 |
 如图是桂林冬季某一天的气温随时间变化的图象,请根据图象填空:在
如图是桂林冬季某一天的气温随时间变化的图象,请根据图象填空:在 如图,直角坐标系中的网格由单位正方形构成.△ABC中,A点坐标为(2,3)、B(-2,0)、C(0,-1).
如图,直角坐标系中的网格由单位正方形构成.△ABC中,A点坐标为(2,3)、B(-2,0)、C(0,-1).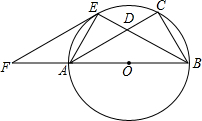 已知:如图,以Rt△ABC的边AB为直径作△ABC的外接圆O,∠B的平分线BE交AC于D,交⊙O于E,作EF∥AC交BA的延长线于F.
已知:如图,以Rt△ABC的边AB为直径作△ABC的外接圆O,∠B的平分线BE交AC于D,交⊙O于E,作EF∥AC交BA的延长线于F.