题目内容
 如图,△ABC中,AB=AC,AD=AE=EB,BC=BE,求∠A的度数.
如图,△ABC中,AB=AC,AD=AE=EB,BC=BE,求∠A的度数.考点:等腰三角形的性质
专题:
分析:首先设∠EBD=°,然后根据等角对等边的性质求得∠A=∠EBD=x,又由三角形外角的性质求得∠BEC,同理,求得∠C=∠BEC,∠C=∠ABC,然后由△ABC的内角和等于180°,列方程求得x的值,则问题得解.
解答:解:设∠EBD=x,
∵AE=EB,
∴∠A=∠EBD=x,
∴∠BEC=∠EBD+∠A=2x,
∵BC=BE,
∴∠C=∠BEC=2x,
∵AB=AC,
∴∠ABC=∠C=2x,
∵∠A+∠ABC+∠C=180°,
即:x+2x+2x=180°,
解得:x=36°,
∴∠A=36°.
∵AE=EB,
∴∠A=∠EBD=x,
∴∠BEC=∠EBD+∠A=2x,
∵BC=BE,
∴∠C=∠BEC=2x,
∵AB=AC,
∴∠ABC=∠C=2x,
∵∠A+∠ABC+∠C=180°,
即:x+2x+2x=180°,
解得:x=36°,
∴∠A=36°.
点评:此题考查了等腰三角形的性质,三角形外角的性质以及三角形内角和定理.此题图形比较复杂,难度适中,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
相关题目
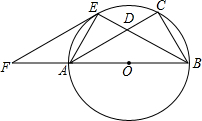 已知:如图,以Rt△ABC的边AB为直径作△ABC的外接圆O,∠B的平分线BE交AC于D,交⊙O于E,作EF∥AC交BA的延长线于F.
已知:如图,以Rt△ABC的边AB为直径作△ABC的外接圆O,∠B的平分线BE交AC于D,交⊙O于E,作EF∥AC交BA的延长线于F. 如图,△ABC≌△ADE,其中B与D,C与E对应,
如图,△ABC≌△ADE,其中B与D,C与E对应,