题目内容
13．
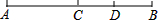如图，C是线段AB的中点，D是线段CB的中点，下列说法错误的是（ ）| A． | CD=AC-BD | B． | CD=$\frac{1}{2}$AB-BD | C． | AC+BD=BC+CD | D． | CD=$\frac{1}{3}$AB |
分析 根据线段中点的性质，可得CD、BD与AB、BC的关系，可得答案．
解答 解：由C是线段AB的中点，D是线段CB的中点，得
AC=CB，CD=DB．
A、CD=CB-BD=AC-BD，故A正确；
B、CD=CB-BD=$\frac{1}{2}$AB-BD，故B正确；
C、AC+BD=BC+CD，故C正确；
D、CD=$\frac{1}{2}$BC=$\frac{1}{4}$AB，故D错误；
故选：D．
点评 本题考查了两点间的距离，利用线段中点的性质得出CD、BD与AB、BC的关系是解题关键．
练习册系列答案
相关题目
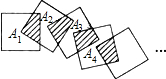将n个边长都为2cm的正方形按如图所示的方法摆放，点A1、A2、…、AN分别是正方形的中心，则2016个这样的正方形重叠部分（阴影部分）的面积和为2015．
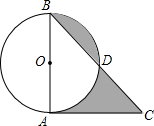如图，AB是⊙O的直径，BD是弦，过点A的切线交BD延长线于点C．若AB=AC=4，则图中阴影部分图形的面积和是4．
如图，△AOB和△ACD均为正三角形，顶点B、D在双曲线y=$\frac{4}{x}$（x＞0）上，则S△OBP=4．
2．下列计算结果为正数的是（ ）
| A． | （-$\frac{1}{2}$）3 | B． | （-$\frac{1}{2}$）-2 | C． | -（-$\frac{1}{2}$）0 | D． | -|$\frac{1}{2}$| |
