题目内容
5.先化简,再求值:(x-2+$\frac{3}{x+2}$)÷$\frac{{x}^{2}+2x+1}{x+2}$,其中x=(π-2017)0-$\sqrt{4}$+($\frac{1}{3}$)-1.分析 原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,求出x的值代入计算即可求出值.
解答 解:原式=[$\frac{(x+2)(x-2)}{x+2}$+$\frac{3}{x+2}$]•$\frac{x+2}{(x+1)^{2}}$=$\frac{(x+1)(x-1)}{x+2}$•$\frac{x+2}{(x+1)^{2}}$=$\frac{x-1}{x+1}$,
当x=1-2+3=2时,原式=$\frac{1}{3}$.
点评 此题考查了分式的化简求值,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.在$\frac{1}{x}$、$\frac{1}{2}$、$\frac{{{x^2}+1}}{2}$、$\frac{3xy}{π}$、$\frac{3}{x+y}$、$a+\frac{1}{b}$中,分式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
16.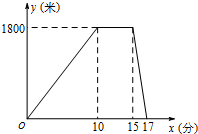 某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中正确的是( )
某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中正确的是( )
 某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中正确的是( )
某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中正确的是( )| A. | 小明在公园休息了15分钟 | B. | 小明乘出租车用了17分 | ||
| C. | 小明跑步的速度为120米/分 | D. | 出租车的平均速度是900米/分 |
15.甲、乙两名射箭运动员在某次测试中各射箭10次,两人的测试成绩如下表,则这两个人本次测试成绩的方差比较( )
| 甲的成绩 | ||||
| 环数 | 7 | 8 | 9 | 10 |
| 频数 | 3 | 2 | 2 | 3 |
| 乙的成绩 | ||||
| 环数 | 7 | 8 | 9 | 10 |
| 频数 | 2 | 3 | 3 | 2 |
| A. | S甲<S乙 | B. | S甲=S乙 | C. | S甲>S乙 | D. | 无法比较 |