题目内容
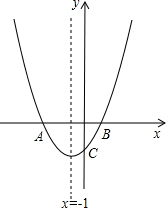 已知一条抛物线与x轴相交于A(-3,0)、B两点,与y轴交于点C(0,-2),其对称轴为x=-1.
已知一条抛物线与x轴相交于A(-3,0)、B两点,与y轴交于点C(0,-2),其对称轴为x=-1.(1)求这条抛物线的解析式;
(2)已知对称轴上存在一点M,使△BCM的周长最小,请求出M点的坐标;
(3)如果将抛物线向右平移1个长度单位得到另一条抛物线,写出这条抛物线的解析式,并求出两条抛物线的交点坐标;
(4)设P(x,y)是第二条抛物线上的一个动点,△PAB的面积为S,求S与x的函数关系式.
考点:二次函数综合题
专题:压轴题
分析:(1)设顶点式解析式为y=a(x+1)2+k,然后把点A、C的坐标代入求出a、k即可;
(2)根据轴对称确定最短路线问题,连接AC与对称轴的交点即为所求的点M,然后利用待定系数法求一次函数解析式求出直线AC的解析式,再求解即可;
(3)根据向右平移横坐标加求出平移后的抛物线的顶点坐标,然后利用顶点式解析式写出即可,再联立两抛物线解析式求解即可得到交点坐标;
(4)令y=0求出点B的坐标,再分点P在x轴下方和上方两种情况,根据三角形的面积公式列式整理即可.
(2)根据轴对称确定最短路线问题,连接AC与对称轴的交点即为所求的点M,然后利用待定系数法求一次函数解析式求出直线AC的解析式,再求解即可;
(3)根据向右平移横坐标加求出平移后的抛物线的顶点坐标,然后利用顶点式解析式写出即可,再联立两抛物线解析式求解即可得到交点坐标;
(4)令y=0求出点B的坐标,再分点P在x轴下方和上方两种情况,根据三角形的面积公式列式整理即可.
解答:解:(1)设抛物线解析式为y=a(x+1)2+k,
将点A、C坐标代入得,
,
解得
.
所以y=
(x+1)2-
;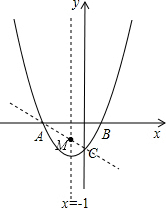
(2)由轴对称确定最短路线问题,直线AC与对称轴的交点即为所求的点M,
设直线AC的解析式为y=kx+b,
则
,
解得
,
所以,直线AC的解析式为y=-
x-2,
当x=-1时,y=-
×(-1)-2=-
,
∴△BCM的周长最小时,点M的坐标为(-1,-
);
(3)原抛物线的顶点坐标为(-1,-
),
∵抛物线向右平移1个长度单位,
∴新抛物线的顶点坐标为(0,-
),
∴这条抛物线的解析式为y=
x2-
,
联立
,
解得
.
所以,两抛物线的交点坐标为(-
,-
);
(4)令y=0,则
(x+1)2-
=0,
解得x1=-3,x2=1,
所以,点B的坐标为(1,0),
∴AB=1-(-3)=1+3=4,
当x<-2或x>-2时,点P在x轴上方,△PAB的面积为S=
×4×(
x2-
)=
x2-
,
当-2<x<2时,点P在x轴下方,△PAB的面积为S=
×4×[-(
x2-
)]=-
x2+
,
当x=-2或x=2时,点P在x轴上,点P、A、B不能构成三角形.
将点A、C坐标代入得,
|
解得
|
所以y=
| 2 |
| 3 |
| 8 |
| 3 |

(2)由轴对称确定最短路线问题,直线AC与对称轴的交点即为所求的点M,
设直线AC的解析式为y=kx+b,
则
|
解得
|
所以,直线AC的解析式为y=-
| 2 |
| 3 |
当x=-1时,y=-
| 2 |
| 3 |
| 4 |
| 3 |
∴△BCM的周长最小时,点M的坐标为(-1,-
| 4 |
| 3 |
(3)原抛物线的顶点坐标为(-1,-
| 8 |
| 3 |
∵抛物线向右平移1个长度单位,
∴新抛物线的顶点坐标为(0,-
| 8 |
| 3 |
∴这条抛物线的解析式为y=
| 2 |
| 3 |
| 8 |
| 3 |
联立
|
解得
|
所以,两抛物线的交点坐标为(-
| 1 |
| 2 |
| 5 |
| 2 |
(4)令y=0,则
| 2 |
| 3 |
| 8 |
| 3 |
解得x1=-3,x2=1,
所以,点B的坐标为(1,0),
∴AB=1-(-3)=1+3=4,
当x<-2或x>-2时,点P在x轴上方,△PAB的面积为S=
| 1 |
| 2 |
| 2 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
当-2<x<2时,点P在x轴下方,△PAB的面积为S=
| 1 |
| 2 |
| 2 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
当x=-2或x=2时,点P在x轴上,点P、A、B不能构成三角形.
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,轴对称确定最短路线问题,联立两函数解析式求交点坐标,三角形的面积,综合题,但难度不大,关键在于(2)判断出点M的位置,(4)根据点P的位置分情况讨论.

练习册系列答案
相关题目
圣诞节期间,某品牌圣诞树按成本价提高50%后标价,再打8折销售,利润为30元.设该圣诞树的成本价为x元,根据题意,下面所列方程正确的是( )
| A、(1+50%)x-x=30 |
| B、80%•(1+50%)x-x=30 |
| C、x-80%x=30 |
| D、50%x•80%=30 |
若直线y=ax+2与直线y=bx-3的交点在x轴上,则
的值为( )
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
 如图,∠AOD=70°,OB是∠AOC的平分线,∠AOB=20°,求∠AOC、∠COD.
如图,∠AOD=70°,OB是∠AOC的平分线,∠AOB=20°,求∠AOC、∠COD. 如图:点C是∠AOB的边OB上的一点,按下列要求画图并回答问题.
如图:点C是∠AOB的边OB上的一点,按下列要求画图并回答问题.