题目内容
1.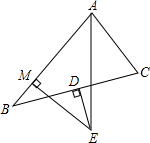 如图,AE平分∠BAC,BD=DC,DE⊥BC,EM⊥AB,若AB=9,AC=5.则AM=( )
如图,AE平分∠BAC,BD=DC,DE⊥BC,EM⊥AB,若AB=9,AC=5.则AM=( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 过点E作EM⊥AC的延长线于点M,连接BE、EC,利用角平分线的性质、垂直平分线的性质得到EM=EN,EB=EC,证明Rt△BME≌Rt△CNE(HL),得到BM=CN,证明Rt△AME≌Rt△ANE(HL),得到AM=AN,由AM=AB-BM=AB-CN=AB-(AN-AC)=AB-AN+AC=AB-AM+AC,即AM=9-AM+5,即可解答.
解答 解:如图,过点E作EM⊥AC的延长线于点M,连接BE、EC,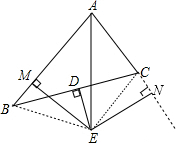
∵BD=DC,DE⊥BC
∵BE=EC.
∵AE平分∠BAC,EM⊥AB,EN⊥AC,
∴EM=EN,∠EMB=∠ENC=90°.
在Rt△BME和Rt△CNE中,
$\left\{\begin{array}{l}{BE=EC}\\{EM=EN}\end{array}\right.$,
∴Rt△BME≌Rt△CNE(HL)
∴BM=CN,
在RtAME和Rt△ANE中,
$\left\{\begin{array}{l}{EM=EN}\\{AE=AE}\end{array}\right.$,
∴Rt△AME≌Rt△ANE(HL)
∴AM=AN,
∴AM=AB-BM=AB-CN=AB-(AN-AC)=AB-AN+AC=AB-AM+AC,
即AM=9-AM+5
2AM=9+5
2AM=14
AM=7.
故选:C.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是证明Rt△BME≌Rt△CNE(HL),得到BM=CN,证明Rt△AME≌Rt△ANE(HL),得到AM=AN.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.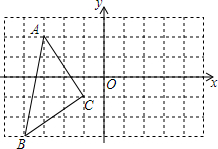 如图,△ABC各顶点坐标是A(-3,2)、B(-4,-3)、C(-1,-1).
如图,△ABC各顶点坐标是A(-3,2)、B(-4,-3)、C(-1,-1).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出线段AC1和线段CC1,并直接写出△ACC1的面积S的值.
 如图,△ABC各顶点坐标是A(-3,2)、B(-4,-3)、C(-1,-1).
如图,△ABC各顶点坐标是A(-3,2)、B(-4,-3)、C(-1,-1).(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出线段AC1和线段CC1,并直接写出△ACC1的面积S的值.
11.下列方程中,是一元一次方程的是( )
| A. | 3x-2y+z=0 | B. | $\frac{x}{7}$=-1 | C. | $\frac{2}{1-x}$=3 | D. | x2-x=1 |
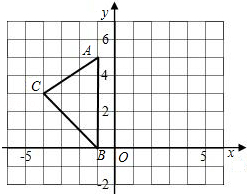 已知:如图,已知△ABC,
已知:如图,已知△ABC,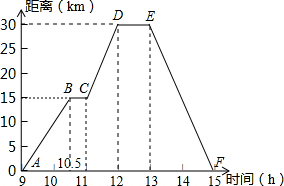 小强骑自行车去郊游,右图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象,小明9点离开家,15点回家.根据这个图象,请你回答下列问题:
小强骑自行车去郊游,右图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象,小明9点离开家,15点回家.根据这个图象,请你回答下列问题: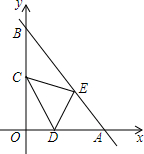 已知:如图,直线y=-x+4分别交x轴、y轴于A、B点,将△AOB折叠,使A点恰好落在OB的中点C处,折痕为DE.
已知:如图,直线y=-x+4分别交x轴、y轴于A、B点,将△AOB折叠,使A点恰好落在OB的中点C处,折痕为DE.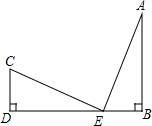 如图,CD⊥DB于D,AB⊥DB于B,CD=EB,AB=ED.求证:CE⊥AE.
如图,CD⊥DB于D,AB⊥DB于B,CD=EB,AB=ED.求证:CE⊥AE.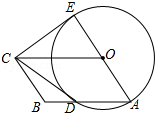 如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD、CE,若CE是⊙O的切线.
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD、CE,若CE是⊙O的切线.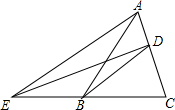 如图.△ABC的面积为6,D为AC边上一点,AD=$\frac{1}{2}$CD,连接BD.过点A作DB的平行线交CB的延长线于点E,连接DE,求△EDB的面积.
如图.△ABC的面积为6,D为AC边上一点,AD=$\frac{1}{2}$CD,连接BD.过点A作DB的平行线交CB的延长线于点E,连接DE,求△EDB的面积.