题目内容
16.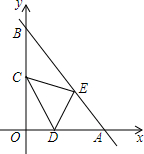 已知:如图,直线y=-x+4分别交x轴、y轴于A、B点,将△AOB折叠,使A点恰好落在OB的中点C处,折痕为DE.
已知:如图,直线y=-x+4分别交x轴、y轴于A、B点,将△AOB折叠,使A点恰好落在OB的中点C处,折痕为DE.(1)求AE的长及sin∠BEC的值;
(2)求△BCE的面积.
分析 (1)作CF⊥BE于F点,由函数解析式可得点B(0,4),点A(4,0),∠A=∠B=45°,设AE=CE=x,表示出EF、CF,然后在Rt△CEF中利用勾股定理可求出x,继而可得出答案.
(2)直接利用S△BCE=$\frac{1}{2}$BE•CF求出答案即可.
解答 解:如图1,作CF⊥BE于F点,由函数解析式可得点B(0,4),点A(4,0),∠A=∠B=45°,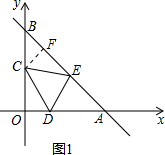
又∵点C是OB中点,
∴OC=BC=2,CF=BF=$\sqrt{2}$,
设AE=CE=x,则EF=AB-BF-AE=4$\sqrt{2}$-$\sqrt{2}$-x,
在RT△CEF中,CE2=CF2+EF2,即x2=(3$\sqrt{2}$-x)2+($\sqrt{2}$)2,
解得:x=$\frac{5\sqrt{2}}{3}$,
故可得sin∠BEC=$\frac{CF}{CE}$=$\frac{3}{5}$,AE=$\frac{5\sqrt{2}}{3}$;
(2)则S△BCE=$\frac{1}{2}$BE•CF=$\frac{1}{2}$×(AB-AE)×CF=$\frac{1}{2}$×$\frac{7\sqrt{2}}{3}$×$\sqrt{2}$=$\frac{7}{3}$.
点评 本题考查了一次函数的综合题,涉及了三角函数、勾股定理、翻折变换的性质及三角形的面积,解答本题的关键是利用勾股定理求出AE的长,此题三角形的面积可以表示为$\frac{1}{2}$absin∠C,(其中∠C是边a、b的夹角).

练习册系列答案
相关题目
5.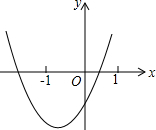 二次函数y=ax2+bx+c的图象如图所示,则下列关于a、b、c间的关系判断正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关于a、b、c间的关系判断正确的是( )
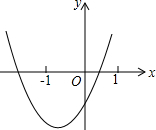 二次函数y=ax2+bx+c的图象如图所示,则下列关于a、b、c间的关系判断正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关于a、b、c间的关系判断正确的是( )| A. | ab<0 | B. | bc>0 | C. | a+b+c>0 | D. | a-b+c>0 |
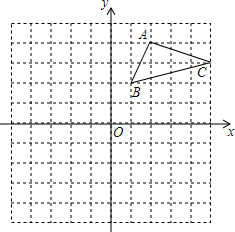 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上, 如图,已知抛物线y=ax2+bx+c(a≠0)经过原点和点(-2,0),则3b-2a<0.(填>、<或=).
如图,已知抛物线y=ax2+bx+c(a≠0)经过原点和点(-2,0),则3b-2a<0.(填>、<或=).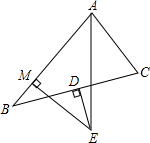 如图,AE平分∠BAC,BD=DC,DE⊥BC,EM⊥AB,若AB=9,AC=5.则AM=( )
如图,AE平分∠BAC,BD=DC,DE⊥BC,EM⊥AB,若AB=9,AC=5.则AM=( )