题目内容
13.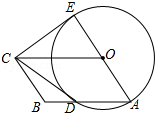 如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD、CE,若CE是⊙O的切线.
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD、CE,若CE是⊙O的切线.(1)求证:CD是⊙O的切线;
(2)若BC=3,CD=4,求∠BAE的正切值.
分析 (1)连接OD,证出△EOC≌△DOC,推出∠ODC=∠OEC=90°,根据切线的判定推出即可;
(2)根据平行四边形的性质得到OC∥AB,由平行线的性质得到∠COD=∠ODA,根据等腰三角形的性质得到∠BAE=∠ODA,等量代换得到∠COD=∠BAE,于是得到结论.
解答 (1)证明:∵CE是⊙O的切线,
∴∠OEC=90°, 如图1,连接OD,
如图1,连接OD,
∵四边形OABC是平行四边形,
∴AO=BC,OC=AB,OC∥AB,
∴∠EOC=∠A,∠COD=∠ODA,
∵OD=OA,
∴∠A=∠ODA,
∴∠EOC=∠DOC,
在△EOC和△DOC中,
$\left\{\begin{array}{l}{OE=OD}\\{∠EOC=∠DOC}\\{OC=OC}\end{array}\right.$,
∴△EOC≌△DOC(SAS),
∴∠ODC=∠OEC=90°,
∴OD⊥CD, ∴CD是⊙O的切线;
∴CD是⊙O的切线;
(2)解:过D作DF⊥OC于F,如图2,
∵四边形OABC是平行四边形,
∴OA=BC=3,
∵OD=OA=BC,
∴∠A=∠ODA,
∵OC∥AB,
∴∠COD=∠ODA,
∴∠FOD=∠A,
∴∠BAE的正切值=$\frac{CD}{OD}$=$\frac{4}{3}$.
点评 本题考查了切线的性质和判定,平行四边形的性质,平行线的性质,勾股定理,三角形的面积的应用,熟练掌握切线的判定和性质是解题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
5.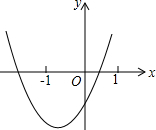 二次函数y=ax2+bx+c的图象如图所示,则下列关于a、b、c间的关系判断正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关于a、b、c间的关系判断正确的是( )
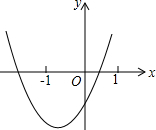 二次函数y=ax2+bx+c的图象如图所示,则下列关于a、b、c间的关系判断正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关于a、b、c间的关系判断正确的是( )| A. | ab<0 | B. | bc>0 | C. | a+b+c>0 | D. | a-b+c>0 |
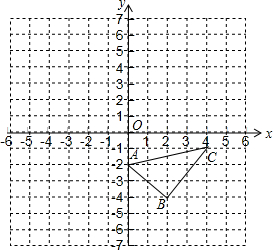 如图,已知△ABC,
如图,已知△ABC, 如图,已知抛物线y=ax2+bx+c(a≠0)经过原点和点(-2,0),则3b-2a<0.(填>、<或=).
如图,已知抛物线y=ax2+bx+c(a≠0)经过原点和点(-2,0),则3b-2a<0.(填>、<或=).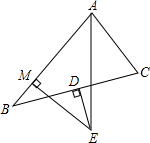 如图,AE平分∠BAC,BD=DC,DE⊥BC,EM⊥AB,若AB=9,AC=5.则AM=( )
如图,AE平分∠BAC,BD=DC,DE⊥BC,EM⊥AB,若AB=9,AC=5.则AM=( )