题目内容
提出命题:如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:四边形ABCD是平行四边形.
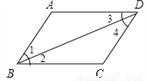
小明提供了如下解答过程:
证明:连接BD.
∵∠1+∠3=180º-∠A,∠2+∠4=180º―∠C,∠A=∠C,
∴ ∠1+∠3=∠2+∠4.
∵∠ABC=∠ADC,
∴∠1=∠4,∠2=∠3.
∴AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
反思交流:(1)请问小明的解法正确吗?如果有错,说明错在何处,并给出正确的证明过程.
(2)用语言叙述上述命题:___________________________________________________.
运用探究:(3)下列条件中,能确定四边形ABCD是平行四边形的是(_____)
A. ∠A∶∠B∶∠C∶∠D=1∶2∶3∶4 B. ∠A∶∠B∶∠C∶∠D=1∶3∶1∶3
C. ∠A∶∠B∶∠C∶∠D=2∶3∶3∶2 D. ∠A∶∠B∶∠C∶∠D=1∶1∶3∶3
 (1)答案见解析;(2)两组对角分别相等的四边形是平行四边形; (3)B
【解析】试题分析:(1)利用四边形的内角和和已知条件中的对角相等得到邻角互补,从而判定两组对边平行,进而证得结论;(2)两组对角分别相等的四边形是平行四边形;(3)由(1)即可得出结论.
【解析】
(1)小明的解法不正确,错在推出∠1+∠3=∠2+∠4后,由∠ABC=∠ADC,不能直接推出∠1=∠4,∠2=...
(1)答案见解析;(2)两组对角分别相等的四边形是平行四边形; (3)B
【解析】试题分析:(1)利用四边形的内角和和已知条件中的对角相等得到邻角互补,从而判定两组对边平行,进而证得结论;(2)两组对角分别相等的四边形是平行四边形;(3)由(1)即可得出结论.
【解析】
(1)小明的解法不正确,错在推出∠1+∠3=∠2+∠4后,由∠ABC=∠ADC,不能直接推出∠1=∠4,∠2=...
 金钥匙试卷系列答案
金钥匙试卷系列答案为改善环境,张村拟在荒山上种植960棵树,由于共青团员的支持,每日比原计划多种20棵,结果提前4天完成任务,原计划每天种植多少棵?设原计划每天种植x棵,根据题意得方程______________.
 【解析】设原计划每天种植x棵,根据题意:
故答案: .
【解析】设原计划每天种植x棵,根据题意:
故答案: . 计算:(1) =________;(2)
=________;(2) =______________.
=______________.
 【解析】试题解析:(1)原式
(2)原式
故答案为:(1) (2) .
【解析】试题解析:(1)原式
(2)原式
故答案为:(1) (2) . 在方程 中,如果设y=x2﹣4x,那么原方程可化为关于y的整式方程是__.
中,如果设y=x2﹣4x,那么原方程可化为关于y的整式方程是__.
 【解析】方程可变形为x2-4x++4=0,因为,所以,整理得,
【解析】方程可变形为x2-4x++4=0,因为,所以,整理得, 若x=-1,y=2,则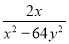 -
-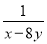 的值为( )
的值为( )
A. -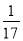 B.
B. 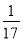 C.
C. 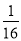 D.
D. 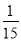
 D
【解析】试题分析:原式====,
当, 时,原式==.故选D.
D
【解析】试题分析:原式====,
当, 时,原式==.故选D. 如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为( ).
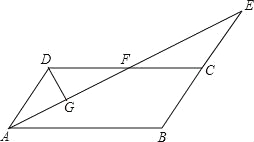
A.2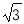 B.4
B.4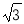 C.4 D.8
C.4 D.8
 B.
【解析】
试题分析:由AE为角平分线,得到一对角相等,再由ABCD为平行四边形,得到AD与BE平行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到AD=DF,由F为DC中点,AB=CD,求出AD与DF的长,得出三角形ADF为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD与DG的长,利用勾股定理求出AG的长,进而求出AF的长,再由三角形AD...
B.
【解析】
试题分析:由AE为角平分线,得到一对角相等,再由ABCD为平行四边形,得到AD与BE平行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到AD=DF,由F为DC中点,AB=CD,求出AD与DF的长,得出三角形ADF为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD与DG的长,利用勾股定理求出AG的长,进而求出AF的长,再由三角形AD... 已知□ABCD中,AB=8 cm,BC=7 cm,则此平行四边形的周长为_________cm.
 30
【解析】平行四边形的周长为(8+7)×2=30cm.
30
【解析】平行四边形的周长为(8+7)×2=30cm. 分式方程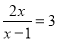 的解是______
的解是______
 3
【解析】去分母得:2x=3x-3,
解得:x=3,
经检验x=3是分式方程的解.
故答案为:x=3
3
【解析】去分母得:2x=3x-3,
解得:x=3,
经检验x=3是分式方程的解.
故答案为:x=3 计算: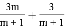 =______.
=______.
 3.
【解析】试题分析:利用同分母分式的加法法则计算即可,即原式==3.
3.
【解析】试题分析:利用同分母分式的加法法则计算即可,即原式==3. 
