Question

3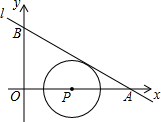．我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：y=kx+4$\sqrt{3}$与x轴、y轴分别交于A、B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA上运动时，使得⊙P成为整圆的点P个数是（　　）

• A． 6
• B． 8
• C． 10
• D． 12

Answer 1

分析 根据直线的解析式求得OB=4$\sqrt{3}$，进而求得OA=12，根据切线的性质求得PM⊥AB，根据∠OAB=30°，求得PM=$\frac{1}{2}$PA，然后根据“整圆”的定义，即可求得使得⊙P成为整圆的点P的坐标，从而求得点P个数．

解答 解：∵直线l：y=kx+4$\sqrt{3}$与x轴、y轴分别交于A、B，
∴B（0，4$\sqrt{3}$），
∴OB=4$\sqrt{3}$，
在RT△AOB中，∠OAB=30°，
∴OA=$\sqrt{3}$OB=$\sqrt{3}$×$4\sqrt{3}$=12，
∵⊙P与l相切，设切点为M，连接PM，则PM⊥AB，
∴PM=$\frac{1}{2}$PA，
设P（x，0），
∴PA=12-x，
∴⊙P的半径PM=$\frac{1}{2}$PA=6-$\frac{1}{2}$x，
∵x为整数，PM为整数，
∴x可以取0，2，4，6，8，10，6个数，
∴使得⊙P成为整圆的点P个数是6．
故选：A．

点评 本题考查了切线的性质，含30°角的直角三角形的性质等，熟练掌握性质定理是解题的关键．