题目内容
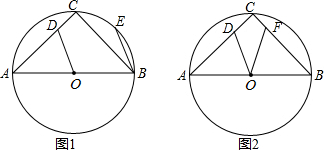
6. 如图所示,AB∥ED,∠CAB=135°,∠ACD=80°,则∠CDE的度数是35°.
如图所示,AB∥ED,∠CAB=135°,∠ACD=80°,则∠CDE的度数是35°.
分析 作CF∥AB,如图,根据平行线的性质,由CF∥AB得到∠CAB+∠ACF=180°,则可计算出∠ACF=45°,所以∠FCD=∠ACD-∠ACF=35°,再利用平行的传递性得到CF∥ED,于是根据平行线的性质即可得到∠CDE=∠FCD=35°.
解答  解:作CF∥AB,如图,
解:作CF∥AB,如图,
∵CF∥AB,
∴∠CAB+∠ACF=180°,
∴∠ACF=180°-135°=45°,
∴∠FCD=∠ACD-∠ACF=80°-45°=35°,
∵AB∥ED,AB∥CF,
∴CF∥ED,
∴∠CDE=∠FCD=35°.
故答案为35°.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.关于x的方程式$\frac{m}{x+1}$=1的解是负数,则m的取值范围是( )
| A. | m>-1 | B. | m≥-1 | C. | m<1且m≠-1 | D. | m<1且m≠0 |
14.已知函数y=|(x-1)2-1|,则使y=k成立的x值恰好有三个,则k的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
11.2014年北京APEC会议期间共有2280名青年志愿者上岗服务,2280用科学记数法表示为( )
| A. | 0.228×104 | B. | 2.28×102 | C. | 2.28×103 | D. | 2.28×104 |
 将△ABC绕点C按逆时针旋转90°,得到△EFC,试画出△EFC的位置.
将△ABC绕点C按逆时针旋转90°,得到△EFC,试画出△EFC的位置.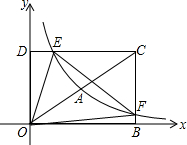 如图,在平面直角坐标系中,矩形DOBC的顶点O与坐标原点重合,B、D分别在坐标轴上,点C的坐标为(6,4),反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.
如图,在平面直角坐标系中,矩形DOBC的顶点O与坐标原点重合,B、D分别在坐标轴上,点C的坐标为(6,4),反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.