题目内容
3.抛物线y=ax2+c的顶点为(0,4),且与抛物线y=$\frac{1}{2}$x2的形状相同,开口相反.(1)求该抛物线的解析式;
(2)求抛物线y=ax2+c与x轴的交点坐标;
(3)当x取何值时,ax2+c>0?
(4)若A(x1,y1),B(x2,y2),在抛物线y=ax2+c上,且x1<x2<0,试比较y1与y2的大小.
分析 (1)两个抛物线形状相同,开口相反说明a互为相反数,再根据顶点坐标即可写出抛物线的解析式.
(2)令y=0解方程即可解决问题.
(3)利用图象法即可解决.
(4))根据抛物线y=-$\frac{1}{2}$x2+4,开口向下,对称轴为y轴,推出x<0时,y随x的增大而增大,由此即可判断.
解答 解:(1)由题意抛物线的解析式为y=-$\frac{1}{2}$x2+4.
(2)对于抛物线y=-$\frac{1}{2}$x2+4,令y=0,得到-$\frac{1}{2}$x2+4=0,解得x=±2$\sqrt{2}$,
∴抛物线y=ax2+c与x轴的交点坐标为(2$\sqrt{2}$,0)或(-2$\sqrt{2}$,0).
(3)由图象可知当-2$\sqrt{2}$<x<2$\sqrt{2}$时,ax2+c>0.
(4)∵抛物线y=-$\frac{1}{2}$x2+4,开口向下,对称轴为y轴,
∴x<0时,y随x的增大而增大,
∴x1<x2<0时,
∴y1<y2.
点评 本题考查二次函数与x轴的交点、二次函数的性质、二次函数与不等式的关系等知识,解题的关键是灵活运用所学知识解决问题,属于基础题,中考常考题型.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
14.二元一次方程x+y=8的一个解是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$ |
18.关于一次函数y=x-1,下列说法:①图象与y轴的交点坐标是(0,-1);②y随x的增大而增大;③图象经过第一、二、三象限; ④直线y=x-1可以看作由直线y=x向右平移1个单位得到.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.一元二次方程(x-1)(x+2)=0的解是( )
| A. | 1 | B. | 1或-2 | C. | -1或2 | D. | -2 |
13.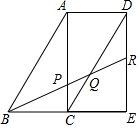 取三个完全相同的三角板拼成如图所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,则BP:PQ:QR=( )
取三个完全相同的三角板拼成如图所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,则BP:PQ:QR=( )
 取三个完全相同的三角板拼成如图所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,则BP:PQ:QR=( )
取三个完全相同的三角板拼成如图所示的形状,R为DE的中点,BR分别交AC,CD于P,Q,则BP:PQ:QR=( )| A. | 3:1:2 | B. | 5:2:3 | C. | 4:1:3 | D. | 6:1:3 |

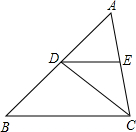 如图,CD平分∠ACB,∠AED=80°,∠DCB=40°,DE与BC平行吗?试说明理由.
如图,CD平分∠ACB,∠AED=80°,∠DCB=40°,DE与BC平行吗?试说明理由.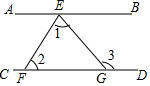 如图,AB∥CD,E是直线AB上的一点,F,G分别是直线CD上的两点,试说明∠3=∠1+∠2.
如图,AB∥CD,E是直线AB上的一点,F,G分别是直线CD上的两点,试说明∠3=∠1+∠2.