题目内容
 为了测量某小球的直径,技术人员将小球放到透明烧杯上,如图是过球心O作为截面图,已知烧杯的高度是13cm,测得l=8cm,h=11cm,则小球的直径为
为了测量某小球的直径,技术人员将小球放到透明烧杯上,如图是过球心O作为截面图,已知烧杯的高度是13cm,测得l=8cm,h=11cm,则小球的直径为考点:垂径定理的应用,勾股定理
专题:
分析:连接AB,过点O作OD⊥AB于点D,根据垂径定理求出BD的长,设小球的半径为r,在Rt△DOB中根据勾股定理求出r的值,进而可得出结论.
解答: 解:如图所示,连接AB,过点O作OD⊥AB于点D,设OB=r,
解:如图所示,连接AB,过点O作OD⊥AB于点D,设OB=r,
∵l=8cm,h=11cm,
∴BD=
×8=4cm.
∵烧杯的高度是13cm,
∴OD=r-(13-11)=r-2,
∴OB2=OD2+BD2,即r2=(r-2)2+42,解得r=5cm,
∴小球的直径为10cm.
故答案为:10.
 解:如图所示,连接AB,过点O作OD⊥AB于点D,设OB=r,
解:如图所示,连接AB,过点O作OD⊥AB于点D,设OB=r,∵l=8cm,h=11cm,
∴BD=
| 1 |
| 2 |
∵烧杯的高度是13cm,
∴OD=r-(13-11)=r-2,
∴OB2=OD2+BD2,即r2=(r-2)2+42,解得r=5cm,
∴小球的直径为10cm.
故答案为:10.
点评:本题考查的是垂径定理,熟知平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
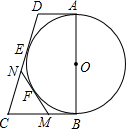 如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O 切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )
如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O 切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )| A、9 | ||
| B、10 | ||
C、3
| ||
D、2
|
下列调查中,不适合用普查的是( )
| A、旅客上飞机前的安检 |
| B、学校招聘教师,对应聘人员的面试 |
| C、了解一批灯泡的使用寿命 |
| D、了解全校学生的课外读书时间 |
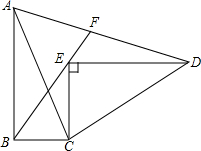 Rt△ABC≌Rt△DEC,∠ABC=∠DEC=90°,BE的延长线交AD于点F,求证:AF=DF.
Rt△ABC≌Rt△DEC,∠ABC=∠DEC=90°,BE的延长线交AD于点F,求证:AF=DF. 如图,圆锥的底面半径为5,母线长为20,一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到点A的最短路程是
如图,圆锥的底面半径为5,母线长为20,一只蜘蛛从底面圆周上一点A出发沿圆锥的侧面爬行一周后回到点A的最短路程是