题目内容
6.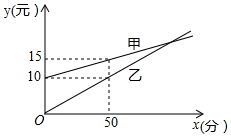 如图所示,是某电信公司甲、乙两种业务:每月通话费用y(元)与通话时间x(分)之间的函数关系.某企业的周经理想从两种业务中选择一种,如果周经理每个月的通话时间都在100分钟以上,那么选择甲种业务合算.
如图所示,是某电信公司甲、乙两种业务:每月通话费用y(元)与通话时间x(分)之间的函数关系.某企业的周经理想从两种业务中选择一种,如果周经理每个月的通话时间都在100分钟以上,那么选择甲种业务合算.
分析 根据函数图象可以分别求得甲、乙两种业务对应的函数解析式,从而可以求得两种花费相同情况时的时刻,然后再根据函数图象即可解答本题.
解答 解:设乙种业务对应的函数解析式为y=kx,
则50k=10,得k=0.2,
即乙种业务对应的函数解析式为y=0.2x,
设甲种业务对应的函数解析式为:y=ax+b,
$\left\{\begin{array}{l}{b=10}\\{50a+b=15}\end{array}\right.$,解得,$\left\{\begin{array}{l}{a=0.1}\\{b=10}\end{array}\right.$,
即甲种业务对应的函数解析式为y=0.1x+10,
∴令0.2x=0.1x+10,得x=100,
即当通话时间为100分钟时两种业务花费一样多,
由图象可知,当通话时间在100分钟以上,甲种业务比较合算,
故答案为:甲.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式,利用函数的性质和数形结合的思想解答.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
3.2015杭州国际动漫节为期6天,某动漫企业准备了卡通玩偶、cosplay道具、动漫手环三类产品参加市集展卖活动,其中动漫手环备货720件,三类产品备货数量的统计图如图甲所示.销售人员(销售卡通玩偶3人,销售cosplay道具1人,销售动漫手环2人)在展卖期间的前3天每人每天销售数量统计图如图乙所示,三类产品前3天的销售总量见表格.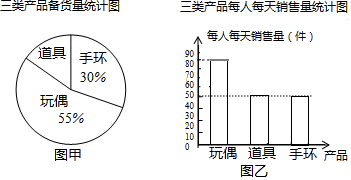
(1)求卡通玩偶、cosplay道具各备货多少件?并直接写出m的值;
(2)若销售人员不变,销售速度相同,请通过计算说明三类产品在展卖期间是否售完?若没有,则求出剩下产品的名称及剩余的数量.

| 产品 | 前三天销售总量(件) |
| 玩偶 | 720 |
| 道具 | m |
| 手环 | 300 |
(2)若销售人员不变,销售速度相同,请通过计算说明三类产品在展卖期间是否售完?若没有,则求出剩下产品的名称及剩余的数量.
 如图,抛物线y=-x2+mx+n与x轴分别交于点A(4.0),B(-2.0).与y轴交于点C
如图,抛物线y=-x2+mx+n与x轴分别交于点A(4.0),B(-2.0).与y轴交于点C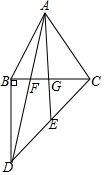 如图,在△ABC中,AB=AC,过点B作BD⊥BC,BD=BC,连接AD交BC于点F.E是CD的中点,连接AE交BC于G.
如图,在△ABC中,AB=AC,过点B作BD⊥BC,BD=BC,连接AD交BC于点F.E是CD的中点,连接AE交BC于G.