题目内容
下列说法正确的是( ).
A. 的平方根是
的平方根是
B.任何数的平方是非负数,因而任何数的平方根也是非负数
C.任何一个非负数的平方根都不大于这个数
D.2是4的平方根
D
【解析】
试题分析:A、根据平方根的定义即可判定;
B、根据平方、平方根的定义即可判定;
C、可以利用反例,如:当0<a<1时结合平方根的定义即可判定;
D、根据平方根的定义即可判定.
A:由于负数没有平方根,故A选项错误;
B:任何数的平方为非负数,正确;但只有非负数才有平方根,且平方根有正负之分(0的平方根为0).故选项B错误;
C:任何一个非负数的平方根都不大于这个数,不一定正确,如:当0<a<1时,a>a2,故选项错误;
D:2的平方是4,所以2是4的平方根,故选项正确.
故选D.
考点:平方根.
考点分析: 考点1:二次根式 二次根式:我们把形如
 叫做二次根式。
叫做二次根式。二次根式必须满足:
含有二次根号“
 ”;
”;被开方数a必须是非负数。
确定二次根式中被开方数的取值范围:
要是二次根式
 有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。
二次根式性质:
有意义,被开方数a必须是非负数,即a≥0,由此可确定被开方数中字母的取值范围。
二次根式性质:(1)a≥0 ;
 ≥0 (双重非负性 );
≥0 (双重非负性 );(2)
 ;
;(3)

0(a=0);
(4)
 ;
;(5)
 。
二次根式判定:
。
二次根式判定:①二次根式必须有二次根号,如
 ,
, 等;
等;②二次根式
 中,被开方数a可以是具体的一个数,也可以是代数式;
中,被开方数a可以是具体的一个数,也可以是代数式;③二次根式定义中a≥0 是定义组成的一部分,不能省略;
④二次根式
 是一个非负数;
是一个非负数;⑤二次根式与算术平方根有着内在的联系,
 (a≥0 )就表示a的算术平方根。
(a≥0 )就表示a的算术平方根。二次根式的应用:
主要体现在两个方面:
(1)利用从特殊到一般,在由一般到特殊的重要思想方法,解决一些规律探索性问题;
(2)利用二次根式解决长度、高度计算问题,根据已知量,求出一些长度或高度,或设计省料的方案,以及图形的拼接、分割问题。这个过程需要用到二次根式的计算,其实就是化简求值。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
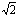 ;当y=4时,x2-1=4,∴x2=5,∴x=±
;当y=4时,x2-1=4,∴x2=5,∴x=±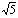 ,故原方程的解为x1=
,故原方程的解为x1=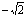 ,x3=
,x3= .
.
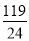 B、
B、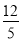 C、
C、 D、
D、
 ×2
×2 ×4
×4 =20
=20



