题目内容
(10分)已知某隧道截面积拱形为抛物线形,拱顶离地面10米,底部款20米.

(1)建立如图1所示的平面直角坐标系,使y轴为抛物线的对称轴,x轴在地面上.求这条抛物线的解析式;
(2)维修队对隧道进行维修时,为了安全,需要在隧道口搭建一个如图2所示的矩形支架AB-BC-CD(其中B、C两点在抛物线上,A、D两点在地面上),现有总长为30米的材料,那么材料是否够用?
(3)在(2)的基础上,若要求矩形支架的高度AB不低于5米,已知隧道是双向行车道,正中间用护栏隔开,则同一方向行驶的两辆宽度分别为4米,高度不超过5米的车能否并排通过隧道口?(护栏宽度和两车间距忽略不计)
(1) ;(2)够用;(3)不能.
;(2)够用;(3)不能.
【解析】
试题分析:(1)设 ,表示出与x轴的一个交点和与y轴的交点,然后利用待定系数法求二次函数解析式解答;
,表示出与x轴的一个交点和与y轴的交点,然后利用待定系数法求二次函数解析式解答;
(2)设点C的坐标为(m,n),然后列式整理得到所需材料表达式,再根据二次函数的最值问题求出所需材料的最大值,然后判断即可;
(3)令n=5求出m的值,然后与车的宽度4米比较即可得解.
试题解析:(1)设 ,
,
由题意抛物线经过点(10,0),(0,10),则 ,解得:
,解得: ,
,
故抛物线的解析式为 ;
;
(2)设点C的坐标为(m,n),
则所需材料长度= ,
,
∵ ,
,
∴当m=5时,所需材料最多,为25米,
∴总长为30米的材料够用;
(3)当 时,
时, ,解得
,解得 ,
,
∵ ,∴高度不超过5米的车不能并排通过隧道口.
,∴高度不超过5米的车不能并排通过隧道口.
考点:1.二次函数综合题;2.二次函数的应用.
考点分析: 考点1:二次函数 定义:一般地,如果
 (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。 ①所谓二次函数就是说自变量最高次数是2;
②二次函数
 (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。③二次函数
 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式: (1)一般式:
 (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0); (2)顶点式:
 (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0) (3)当抛物线
 与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。 二次函数的一般形式的结构特征:
①函数的关系式是整式;
②自变量的最高次数是2;
③二次项系数不等于零。 二次函数的判定:
二次函数的一般形式中等号右边是关于自变量x的二次三项式;
当b=0,c=0时,y=ax2是特殊的二次函数;
判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成
 (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
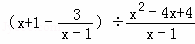 ,其中x满足方程:x2+x﹣6=0。
,其中x满足方程:x2+x﹣6=0。

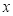 的方程
的方程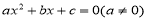 的一个解
的一个解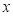 的范围是
的范围是  <3.24 B、3.24<
<3.24 B、3.24< ,b>
,b> ,则a+b的最小值是( )
,则a+b的最小值是( ) 的平方根是
的平方根是

 的图象如图所示,OA=OC,则下列结论:①
的图象如图所示,OA=OC,则下列结论:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ ;⑥
;⑥ .其中正确的有( )
.其中正确的有( )
