题目内容
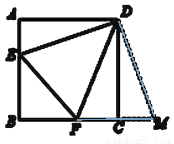
如图,将长为12,宽为5的矩形纸片ABCD沿对角线AC对折后,AD与BC交于点E,则DE的长度 ( )

A、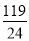 B、
B、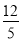 C、
C、 D、
D、
A
【解析】
试题分析:设ED=x,AE=12﹣x,在Rt△AEB′中根据勾股定理即可解出x的值.
如图所示设ED=x,AE=12﹣x,
∵∠ACB=∠ACE
又∵AD∥BC
∴∠ACB=∠EAC
∴∠EAC=∠ACE
∴AE=CE=12﹣x
∵在直角△CDE中,CE2=DE2+CD2
即:(12﹣x)2=x2+25
解得:x=
故答案为

故选A
考点:1.翻折变换(折叠问题);2.勾股定理;3.矩形的性质.
考点分析: 考点1:四边形 四边形:四边形的初中数学中考中的重点内容之一,分值一般为10-14分,题型以选择,填空,解答证明或融合在综合题目中为主,难易度为中。主要考察内容:①多边形的内角和,外角和等问题②图形的镶嵌问题③平行四边形,矩形,菱形,正方形,等腰梯形的性质和判定。突破方法:①掌握多边形,四边形的性质和判定方法。熟记各项公式。②注意利用四边形的性质进行有关四边形的证明。③注意开放性题目的解答,多种情况分析。 考点2:解直角三角形 (1)解直角三角形的定义在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
(2)解直角三角形要用到的关系
①锐角直角的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:
sinA=∠A的对边斜边=ac,cosA=∠A的邻边斜边=bc,tanA=∠A的对边∠A的邻边=ab.
(a,b,c分别是∠A、∠B、∠C的对边) 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 的周长=________.
的周长=________.


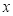 的方程
的方程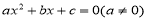 的一个解
的一个解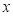 的范围是
的范围是  <3.24 B、3.24<
<3.24 B、3.24< -
- ;
;  -
- .;
.;
 的平方根是
的平方根是
 的值,使二次函数
的值,使二次函数
 的图象同时足下列条件:①开口向下,②当x<-2时,
的图象同时足下列条件:①开口向下,②当x<-2时, 随
随 的增大而增大;当x>-2时,
的增大而增大;当x>-2时, 随
随 的增大而减小.这样的二次函数的解析式可以是 .
的增大而减小.这样的二次函数的解析式可以是 .