题目内容
2.先化简,再求值:$\frac{{x}^{2}-2x+1}{3+4x+{x}^{2}}×\frac{3+x}{{x}^{2}-1}-\frac{1}{1+x}$,其中x满足x2+2x-7=0.分析 先根据题意得出x2+2x=7,再根据分式混合运算的法则把原式进行化简,把x2+2x的值代入进行计算即可.
解答 解:∵x2+2x-7=0,
∴x2+2x=7.
原式=$\frac{(x-1)^{2}}{(x+1)(x+3)}$•$\frac{x+3}{(x+1)(x-1)}$-$\frac{1}{x+1}$
=$\frac{x-1}{(x+1)^{2}}$-$\frac{1}{x+1}$
=$\frac{x-1-(x+1)}{{(x+1)}^{2}}$
=$\frac{x-1-x-1}{{(x+1)}^{2}}$
=$\frac{-2}{{x}^{2}+2x+1}$,
当x2+2x=7时,原式=$\frac{-2}{7+1}$=-$\frac{1}{4}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
13.-(-2)-2=( )
| A. | -4 | B. | 4 | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
7. 如图所示的两个几何体都是由若干个相同的小正方体搭成的,在它们的三视图中,相同的视图是( )
如图所示的两个几何体都是由若干个相同的小正方体搭成的,在它们的三视图中,相同的视图是( )
 如图所示的两个几何体都是由若干个相同的小正方体搭成的,在它们的三视图中,相同的视图是( )
如图所示的两个几何体都是由若干个相同的小正方体搭成的,在它们的三视图中,相同的视图是( )| A. | 主视图 | B. | 左视图 | C. | 俯视图 | D. | 三视图 |
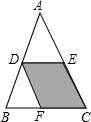 如图,在△ABC中,D、E分别是边AB、AC的中点,连接DE,将△ADE沿AB方向平移到△DBF的位置,点D在BC上,已知△ADE的面积为1,则四边形CEDF的面积是2.
如图,在△ABC中,D、E分别是边AB、AC的中点,连接DE,将△ADE沿AB方向平移到△DBF的位置,点D在BC上,已知△ADE的面积为1,则四边形CEDF的面积是2.
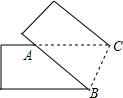 将一张宽为4cm的矩形纸片折叠成如图所示图形,若AB=6cm,则AC的长度为6cm.
将一张宽为4cm的矩形纸片折叠成如图所示图形,若AB=6cm,则AC的长度为6cm.