题目内容
12.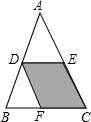 如图,在△ABC中,D、E分别是边AB、AC的中点,连接DE,将△ADE沿AB方向平移到△DBF的位置,点D在BC上,已知△ADE的面积为1,则四边形CEDF的面积是2.
如图,在△ABC中,D、E分别是边AB、AC的中点,连接DE,将△ADE沿AB方向平移到△DBF的位置,点D在BC上,已知△ADE的面积为1,则四边形CEDF的面积是2.
分析 由题可知△ADE∽△ABC相似且相似比是1:2,根据相似比求面积比;然后再由平移的性质来求四边形CEDF的面积:S四边形CEDF=S四边形DBCE-S△ADE.
解答  解:∵如图,将△ADE沿AB方向平移到△DBF的位置,点D在BC上,△ADE的面积为1,
解:∵如图,将△ADE沿AB方向平移到△DBF的位置,点D在BC上,△ADE的面积为1,
∴S△DBF=S△ADE=1.
∵D,E分别是AB,AC的中点,
∴DE∥BC,
∴△ADE∽△ABC,
∴$\frac{S△ADE}{{S}_{△ABC}}$=($\frac{AD}{AB}$)2,即$\frac{1}{{S}_{△ABC}}$=($\frac{1}{2}$)2=$\frac{1}{4}$,
故S△ABC=4,
∴S四边形DBCE=3,
∴S四边形CEDF=S四边形DBCE-S△ADE=3-1=2.
故答案是:2.
点评 本题考查平移的性质和相似三角形的判定与性质,此题利用相似三角形面积的比等于相似比的平方求得S四边形DBCE=3是解题的难点.

练习册系列答案
相关题目
7.下列计算错误的是( )
| A. | $1÷6×\frac{1}{6}=\frac{1}{36}$ | B. | (-2)-2=4 | C. | $\frac{1}{3}-2-(-2\frac{1}{3})=\frac{2}{3}$ | D. | 20150=1 |
4.为了控制房价,最近很多城市出台了房产购买限制措施,假设某人购买某处房子原来需支付首付款30%,即27万元,现在按照新规定首付款必须不低于50%,则这个人按照新规定至少支付首付款( )
| A. | 13.5万元 | B. | 45万元 | C. | 54万元 | D. | 100万元 |
1.下列运算中正确的是( )
| A. | π0=1 | B. | $\sqrt{x^2}=x$ | C. | 2-2=-4 | D. | -|-2|=2 |

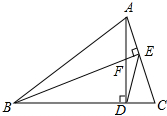 如图,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F,连接DE.
如图,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F,连接DE.