题目内容
7.如图,数轴上有两点A、B,对应的数分别为-2,4,点P为数轴上一动点,其对应的数为x.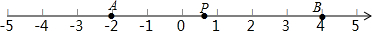
(1)若点P到点A、点B的距离相等,求点P对应的x的值.
(2)数轴上是否存在点P,使得点P到点A、点B的距离之和为10?若存在,请求出x的值;若不存在,说明理由.
(3)点A、B分别以3个单位长度/分,2个单位长度/分的速度向右运动,同时点P以4个单位长度/分的速度从O点向左运动,当遇到A时,点P立即以同样的速度向右运动,并不停往返于点A与点B之间,求当点A与点B重合时,点P所经过的总路程是多少?
分析 (1)根据点P到点A、点B的距离相等列出方程x-(-2)=4-x,解方程即可;
(2)根据PA+PB=10列出方程|x-(-2)|+|4-x|=10,解方程即可;
(3)设经过x分钟点A与点B重合,根据点A比点B运动的距离多6,列出方程,求出x的值,即为点P运动的时间,再乘以点P运动的速度,可得点P点P所经过的总路程.
解答 解:(1)∵点P到点A、点B的距离相等,
∴x-(-2)=4-x,
解得x=1
答:点P对应的数是1.
(2)由题意,得|x-(-2)|+|4-x|=10,即|x+2|+|4-x|=10,
如果x≤-2,得-x-2+4-x=10,解得x=-4;
如果-2<x≤4,得x+2+4-x=10,x无解;
如果x>4,得x+2+x-4=10,解得x=6;
答:数轴上存在点P,使得点P到点A、点B的距离之和为10,此时x的值为6或-4;
(3)设经过a分钟点A与点B重合,根据题意得:
3a=6+2a,
解得a=6.
6×4=24.
答:点P所经过的总路程为24个单位长度.
点评 此题考查一元一次方程的实际运用,利用数轴,结合行程问题找出等量关系,列出方程解决问题.

练习册系列答案
相关题目
2.给出下列判断:
①若|-a|=a,则a<0;
②有理数包括整数、0和分数;
③任何正数都大于它的倒数;
④2ax2-xy+y2是三次三项式;
⑤几个有理数相乘,当负因数的个数是奇数时,积一定为负.
上述判断正确的有( )
①若|-a|=a,则a<0;
②有理数包括整数、0和分数;
③任何正数都大于它的倒数;
④2ax2-xy+y2是三次三项式;
⑤几个有理数相乘,当负因数的个数是奇数时,积一定为负.
上述判断正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
12.下列方程是一元二次方程的是( )
| A. | x2+2xy+y2=0 | B. | x(x+3)=x2-1 | C. | (x-1)(x-3)=0 | D. | $x+\frac{1}{x}=0$ |
16.有苹果若干,分给小朋友吃,若每个小朋友分3个则剩1个,若每个小朋友分4个则少2个,设共有苹果x个,则可列方程为( )
| A. | 3x+4=4x-2 | B. | $\frac{x+1}{3}$=$\frac{x-2}{4}$ | C. | $\frac{x-1}{3}$=$\frac{x+2}{4}$ | D. | $\frac{x+2}{3}$=$\frac{x-1}{4}$ |
 如图,已知等边△ABC中,∠B、∠C的平分线相交于点O,E,F为线段BC上两点,且BE=OE,CF=OF,连接OE、OF,试说明△OEF是等边三角形.
如图,已知等边△ABC中,∠B、∠C的平分线相交于点O,E,F为线段BC上两点,且BE=OE,CF=OF,连接OE、OF,试说明△OEF是等边三角形. 如图所示,已知OE平分△AOB,OD平分∠BOC,∠AOB为直角,∠COD=20°,求∠EOC的度数.
如图所示,已知OE平分△AOB,OD平分∠BOC,∠AOB为直角,∠COD=20°,求∠EOC的度数. 如图,∠AOP=∠BOP=15°,PC∥OA,PQ⊥OA,若PC=4,则PQ=2.
如图,∠AOP=∠BOP=15°,PC∥OA,PQ⊥OA,若PC=4,则PQ=2.