题目内容
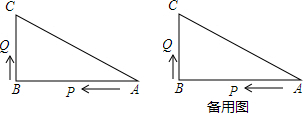
13.如图1,在△ABC中,AB=AC,点D,E分别在AB和AC上,且∠ADC=∠AEB=90°,则CD=BE.探究发现:
如图2,在△ABC中,仍然有条件“AB=AC,点D,E分别在AB和AC上”.若∠ADC+∠AEB=180°,则CD与BE是否仍相等?若相等,请证明;若不相等,请举反例说明.
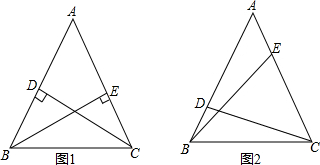
分析 分别作CF⊥AB,BG⊥AC,先证得△FBC≌△GCB,得出CF=BG,进而证得△CFD≌△BGE即可证得CD=BE.
解答  解:CD=BE.
解:CD=BE.
证明如下:如图2,分别作CF⊥AB,BG⊥AC,
∴∠CBF=90°,∠BGC=90°.
∵AB=AC,
∴∠ABC=∠ACB,
在△FBC和△GCB中,
$\left\{\begin{array}{l}{∠CBF=∠BGC}\\{∠ABC=∠ACB}\\{BC=BC}\end{array}\right.$,
∴△FBC≌△GCB(AAS).
∴CF=BG,
∵∠ADC+∠AEB=180°,
又∵∠BEG+∠AEB=180°,
∴∠ADC=∠BEG,
在△CFD和△BGE中,
$\left\{\begin{array}{l}{∠CFD=∠BGE=90°}\\{∠ADC=∠BEG}\\{CF=BG}\end{array}\right.$,
∴△CFD≌△BGE(AAS),
∴CD=BE.
点评 本题考查了三角形全等的判定和性质,作出辅助线构建全等三角形是解题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
15. 如图,已知正方形B的面积为144,正方形C的面积为169时,那么正方形A的面积为( )
如图,已知正方形B的面积为144,正方形C的面积为169时,那么正方形A的面积为( )
 如图,已知正方形B的面积为144,正方形C的面积为169时,那么正方形A的面积为( )
如图,已知正方形B的面积为144,正方形C的面积为169时,那么正方形A的面积为( )| A. | 313 | B. | 144 | C. | 169 | D. | 25 |
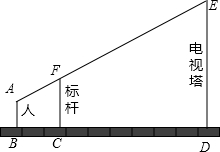 如图,某测量工作人员与标杆顶端F、电视塔顶端在同一直线上,已知此人眼睛距地面1.6米,标杆为3.2米,且BC=1米,CD=5米,则电视塔的高ED=11.2.
如图,某测量工作人员与标杆顶端F、电视塔顶端在同一直线上,已知此人眼睛距地面1.6米,标杆为3.2米,且BC=1米,CD=5米,则电视塔的高ED=11.2. 如图,某次台风把一棵大树在离地面3米处的B点拦腰刮断,大树顶端着地点A到树根部C的距离为4米,那么这棵树的高度是8米.
如图,某次台风把一棵大树在离地面3米处的B点拦腰刮断,大树顶端着地点A到树根部C的距离为4米,那么这棵树的高度是8米.