题目内容
 如图,在△ABC中,∠C=90°,AB=10,AC=8,
如图,在△ABC中,∠C=90°,AB=10,AC=8,(1)若AD为CB边中线,求AD长;
(2)若AD平分∠BAC,求D到AB的距离.
考点:勾股定理,角平分线的性质
专题:
分析:(1)首先利用整式的乘法BC长,再根据中线定义可得CD长,再根据勾股定理计算出AD长;
(2)首先过D作DH⊥AB,根据角平分线的性质可得DH=CD.
(2)首先过D作DH⊥AB,根据角平分线的性质可得DH=CD.
解答: 解:(1)∵∠C=90°,AB=10,AC=8,
解:(1)∵∠C=90°,AB=10,AC=8,
∴BC=
=6,
∵AD为CB边中线,
∴CD=3,
∴AD=
=
=
;
(2)过D作DH⊥AB,
∵AD平分∠BAC,
∴DH=CD=3.
∴D到AB的距离为3.
 解:(1)∵∠C=90°,AB=10,AC=8,
解:(1)∵∠C=90°,AB=10,AC=8,∴BC=
| 102-82 |
∵AD为CB边中线,
∴CD=3,
∴AD=
| AC2+CD2 |
| 64+9 |
| 73 |
(2)过D作DH⊥AB,
∵AD平分∠BAC,
∴DH=CD=3.
∴D到AB的距离为3.
点评:此题主要考查了勾股定理,以及角平分线的性质,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
相关题目
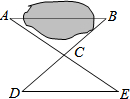 如图,有一池塘,要测量池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长至E,使CE=AC,连结BC并延长至D,使CD=BC,连结DE,根据△ABC≌△EDC可知,量出DE的长,就是A、B的距离,这里△ABC≌△EDC的依据是( )
如图,有一池塘,要测量池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长至E,使CE=AC,连结BC并延长至D,使CD=BC,连结DE,根据△ABC≌△EDC可知,量出DE的长,就是A、B的距离,这里△ABC≌△EDC的依据是( )| A、SAS | B、ASA |
| C、AAS | D、SSS |
根据下列表格中列出来的数值,可判断方程x2-bx-c=0有一个根大约是( )
| x | 0 | 0.5 | 1 | 1.5 | 2 |
| x2-bx-c | -15 | -8.75 | -2 | 5.25 | 13 |
| A、0.25 | B、0.75 |
| C、1.25 | D、1.75 |
 如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.
如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE. 一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是
一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是 如图所示,小明想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开与旗杆底部相距5米后,发现下端刚好接触地面.请你求出旗杆的高度.
如图所示,小明想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开与旗杆底部相距5米后,发现下端刚好接触地面.请你求出旗杆的高度.