题目内容
6.阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,
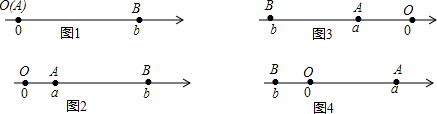
如图1,|AB|=|OB|=|b|=|a-b|;
当A、B两点都不在原点时,
如图2,点A、B都在原点的右边
|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
如图3,点A、B都在原点的左边,
|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;
如图4,点A、B在原点的两边,
|AB|=|OB|+|OA|=|a|+|b|=a+(-b)=|a-b|;
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是3,数轴上表示-2和-5的两点之间的距离是3,数轴上表示1和-3的两点之间的距离是4.
(2)数轴上表示x和-1的两点A和B之间的距离是|x+1|,如果|AB|=2,那么x为1或-3;
(3)当代数式|x+1|+|x-2|取最小值时,相应的x的取值范围是-1≤x≤2.
分析 审题可知题中通过探索已经得出数轴上两点之间的距离求值方法:即两数之差的绝对值,
(1)求两点距离,我们根据题意代入求值即可.
(2)第一个问题只需把字母和数代入即可,第二个问题,根据题意列出方程求解即可.
(3)将绝对值理解为两点之间的距离,再根据两点之间线段最短分析即可.
解答 解:(1)数轴上表示2和5的两点之间的距离是:|2-5|=3,数轴上表示-2和-5的两点之间的距离是:|-2-(-5)|=3,
数轴上表示1和-3的两点之间的距离是:|1-(-3)|=4.
故答案为:3,3,4
(2)数轴上表示x和-1的两点A和B之间的距离是:|x-(-1)|=|x+1|,
由|AB|=2得:|x+1|=2,所以有:x+1=2,或x+1=-2,解得x=1,或x=-3.
故答案为:|x+1|,1或-3.
(3)|x+1|+|x-2|可以看作:表示x的点到表示-1的点和到表示2的点的距离的和,根据两点之间线段最短,可知表示x的点在表示-1的点和到表示2的点的线段上,所以-1≤x≤2.
故答案为:-1≤x≤2.
点评 此题主要考察数轴上两点之间的距离,准确把握题中距离公式并认真代入计算是解题的关键,解题中要注意:由距离求点时,要分类讨论避免漏解.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
17.关于对位似图形的表述,下列命题正确的有( )
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形;
④位似图形上任意一组对应点P,P′与位似中心O的距离满足OP=k•OP′.
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形;
④位似图形上任意一组对应点P,P′与位似中心O的距离满足OP=k•OP′.
| A. | ①②③④ | B. | ②③④ | C. | ②③ | D. | ②④ |
1.下列多项式能用平方差公式因式分解的是( )
| A. | a2+b2 | B. | -a2-b2 | C. | (-a2)+(-b)2 | D. | (-a)2+(-b)2 |