题目内容
3.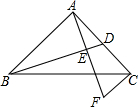 如图,AB⊥AC,AB=AC=$\sqrt{2}$cm,D为AC中点,CF∥AB,AF⊥BD,垂足为E.则CF=$\frac{\sqrt{2}}{2}$cm.
如图,AB⊥AC,AB=AC=$\sqrt{2}$cm,D为AC中点,CF∥AB,AF⊥BD,垂足为E.则CF=$\frac{\sqrt{2}}{2}$cm.
分析 求出∠BAD=∠ACF=90°,根据三角形内角和定理求出∠BAD=∠CAF,根据ASA推出△ABD≌△CDF,根据全等三角形的性质得出AD=CF即可.
解答 解:∵AB⊥AC,CF∥AB,
∴CF⊥AC,
∴∠BAD=∠ACF=90°,
∵AF⊥BD,
∴∠AEB=∠AED=90°,
∴∠ABD+∠ADB=∠CAF+∠ADB=90°,
∴∠BAD=∠CAF,
在△ABD和△CAF中,
$\left\{\begin{array}{l}{∠ABD=∠CAF}\\{AB=AC}\\{∠BAD=∠ACF}\end{array}\right.$,
∴△ABD≌△CDF(ASA),
∴AD=CF,
∵AC=$\sqrt{2}$cm,D为AC中点,
∴AD=$\frac{1}{2}$AC=$\frac{\sqrt{2}}{2}$,
∴CF=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查了全等三角形的性质和判定,平行线的性质,三角形内角和定理的应用,能推出△ABD≌△CDF是解此题的关键,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应角相等,对应边相等.

练习册系列答案
相关题目
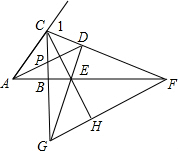 如图,Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠ACB的外角平分线CF相交于点D,AD交CB于P,CF交AB的延长线于F,过D作DE⊥CF交CB的延长线于点G,交AB的延长线于点E,连接CE并延长线交FG于点H,则下列结论:①∠CDA=45°;②AF-CG=CA;③DE=DC;④FH=CD+GH;⑤CF=2CD+EG,其中正确的有①②③⑤.
如图,Rt△ABC中,∠CBA=90°,∠CAB的角平分线AP和∠ACB的外角平分线CF相交于点D,AD交CB于P,CF交AB的延长线于F,过D作DE⊥CF交CB的延长线于点G,交AB的延长线于点E,连接CE并延长线交FG于点H,则下列结论:①∠CDA=45°;②AF-CG=CA;③DE=DC;④FH=CD+GH;⑤CF=2CD+EG,其中正确的有①②③⑤.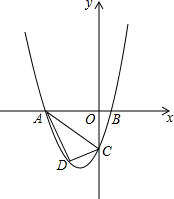 已知,如图,抛物线y=ax2+2ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
已知,如图,抛物线y=ax2+2ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.