题目内容
18.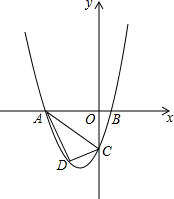 已知,如图,抛物线y=ax2+2ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
已知,如图,抛物线y=ax2+2ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
分析 (1)根据OC=3OB,B(1,0),求出C点坐标(0,-3),把点B,C的坐标代入y=ax2+2ax+c,求出a点坐标即可求出函数解析式;
(2)图,过点D作DM∥y轴分别交线段AC和x轴于点M,N.设M(m,-m-3)则D(m,m2+2m-3),然后求出DM的表达式,把S四边形ABCD分解为S△ABC+S△ACD,转化为二次函数求最值;
(3)①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,此时四边形ACP1E1为平行四边形.平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形.
解答 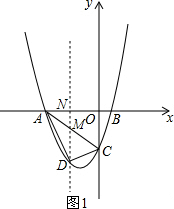 解:(1)∵OC=3OB,B(1,0),
解:(1)∵OC=3OB,B(1,0),
∴C(0,-3).
把点B,C的坐标代入y=ax2+2ax+c,得a=1,c=-3,
∴抛物线的解析式y=x2+2x-3.
(2)由A(-3,0),C(0,-3)得直线AC的解析式为y=-x-3,
如图1,过点D作DM∥y轴分别交线段AC和x轴于点M,N.
设M(m,-m-3)则D(m,m2+2m-3),
DM=-m-3-(m2+2m-3)=-m2-3m=-(m+$\frac{3}{2}$)2+$\frac{9}{4}$,
∴-1<0,
∴当x=$-\frac{3}{2}$时,DM有最大值$\frac{9}{4}$,
∴S四边形ABCD=S△ABC+S△ACD=$\frac{1}{2}$×4×3+$\frac{1}{2}$×3×DM,此时四边形ABCD面积有最大值为6+$\frac{3}{2}$×$\frac{9}{4}$=$\frac{75}{8}$.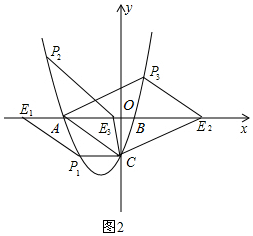 (3)存在.
(3)存在.
讨论:①如图2,过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,
此时四边形ACP1E1为平行四边形.
∵C(0,-3),令-3=x2+2x-3
∴x1=0,x2=-2.
∴P1(-2,-3).
②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,
∵C(0,-3),
∴可令P(x,3),3=x2+2x-3,得x2+2x-6=0
解得x1=-1+$\sqrt{7}$,x2=-1-$\sqrt{7}$,
此时存在点P2(-1+$\sqrt{7}$,3),P3(-1-$\sqrt{7}$,3),
综上所述,存在3个点符合题意,坐标分别是:
P1(-2,-3),P2(-1+$\sqrt{7}$,3),P3(-1-$\sqrt{7}$,3).
点评 本题考查了二次函数综合题,涉及待定系数法求二次函数的解析式,二次函数求最值,平行四边形的判定与性质等知识,根据题意作出图形,利用数形结合求解是解答此题的关键,在解答(3)时要注意进行分类讨论.

 名校课堂系列答案
名校课堂系列答案| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 平均分 | 方差 | |
| 小孙 | 75 | 90 | 75 | 90 | 70 | 70 | |
| 小周 | 70 | 80 | 80 | 90 | 80 | 80 |
(2)根据以上信息,若你是数学老师,你会选择谁参加比赛,为什么?
| A. | 3ab+3ac=6abc | B. | 4a2b-4b2a=0 | C. | 2x2+5x2=7x4 | D. | 5y2-2y2=3y2 |
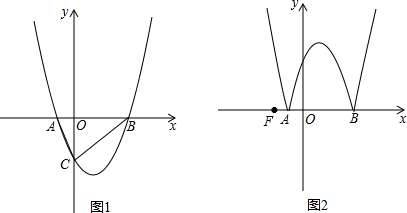
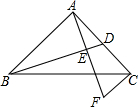 如图,AB⊥AC,AB=AC=$\sqrt{2}$cm,D为AC中点,CF∥AB,AF⊥BD,垂足为E.则CF=$\frac{\sqrt{2}}{2}$cm.
如图,AB⊥AC,AB=AC=$\sqrt{2}$cm,D为AC中点,CF∥AB,AF⊥BD,垂足为E.则CF=$\frac{\sqrt{2}}{2}$cm.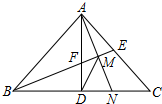 如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,AM的延长线交BC于点N,连接DM,下列结论:①DF=DN; ②△DMN为等腰三角形;③DM平分∠BMN;④AE=$\frac{2}{3}$EC;
如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,AM的延长线交BC于点N,连接DM,下列结论:①DF=DN; ②△DMN为等腰三角形;③DM平分∠BMN;④AE=$\frac{2}{3}$EC;