题目内容
计算:当m为何值时,关于x的方程
+
=
会产生增根?
| 2 |
| x+1 |
| 5 |
| 1-x |
| m |
| x2-1 |
考点:分式方程的增根
专题:
分析:根据等式的性质,可得整式方程,根据分式方程的增根是整式方程的解,可得关于m的方程,根据解方程,可得答案.
解答:解:方程得两边都乘以(x+1)(x-1),得
2(x-1)-5(x+1)=m.
化简,得
m=-3x-7.分式方程的增根是x=1或x=-1.
当x=1时,m=-3-7=-10,
当x=-1时,m=3-7=-4,
当m=-10或m=-4时,关于x的方程
+
=
会产生增根.
2(x-1)-5(x+1)=m.
化简,得
m=-3x-7.分式方程的增根是x=1或x=-1.
当x=1时,m=-3-7=-10,
当x=-1时,m=3-7=-4,
当m=-10或m=-4时,关于x的方程
| 2 |
| x+1 |
| 5 |
| 1-x |
| m |
| x2-1 |
点评:本题考查了分式方程的增根,利用分式方程的增根满足整式方程得出关于m的方程是解题关键.

练习册系列答案
相关题目
设⊙O的半径是6cm,点O到直线l的距离为d,⊙O与直线l有公共点,则( )
| A、d>6cm |
| B、d=6cm |
| C、0≤d<6cm |
| D、0≤d≤6cm |
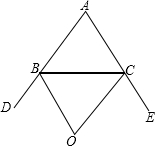 如图:在△ABC中,点O是外角∠DBC和∠ECB的平分线BO,CO的交点,则∠BOC与∠A有怎样的关系?请说明理由.
如图:在△ABC中,点O是外角∠DBC和∠ECB的平分线BO,CO的交点,则∠BOC与∠A有怎样的关系?请说明理由. 已知直线AB、CD、EF交于点O,若∠1=15°,∠2=95°,求∠3的度数.
已知直线AB、CD、EF交于点O,若∠1=15°,∠2=95°,求∠3的度数. 从一个直径为4
从一个直径为4