题目内容
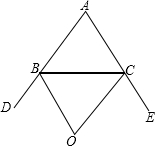 如图:在△ABC中,点O是外角∠DBC和∠ECB的平分线BO,CO的交点,则∠BOC与∠A有怎样的关系?请说明理由.
如图:在△ABC中,点O是外角∠DBC和∠ECB的平分线BO,CO的交点,则∠BOC与∠A有怎样的关系?请说明理由.考点:三角形内角和定理,三角形的外角性质
专题:
分析:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠CBD=∠A+∠ACB,∠BCE=∠A+∠ABC,再根据角平分线的定义和三角形的内角和定理表示出∠OBC+∠OCB,然后利用三角形的内角和定理整理即可得解.
解答:解:由三角形的外角性质得,∠CBD=∠A+∠ACB,∠BCE=∠A+∠ABC,
∵点O是外角∠DBC和∠ECB的平分线BO,CO的交点,
∴∠OBC+∠OCB=
(∠CBD+∠BCE)=
(∠A+∠ACB+∠A+∠ABC),
在△ABC中,∠A+∠ACB+∠ABC=180°,
∴∠OBC+∠OCB=
(180°+∠A),
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-
(180°+∠A)=90°-
∠A,
即∠BOC=90°-
∠A.
∵点O是外角∠DBC和∠ECB的平分线BO,CO的交点,
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
在△ABC中,∠A+∠ACB+∠ABC=180°,
∴∠OBC+∠OCB=
| 1 |
| 2 |
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-
| 1 |
| 2 |
| 1 |
| 2 |
即∠BOC=90°-
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记性质与定理是解题的关键,难点在于整体思想的利用.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠B=90°,AC=40cm,AB=24cm,点D从点C出发沿CA方向以5cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以3cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤8).过点D作DF⊥BC于点F,连接DE,EF.
如图,在Rt△ABC中,∠B=90°,AC=40cm,AB=24cm,点D从点C出发沿CA方向以5cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以3cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤8).过点D作DF⊥BC于点F,连接DE,EF.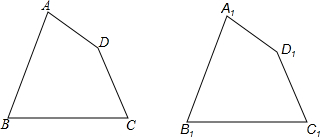
 如图,角的顶点是
如图,角的顶点是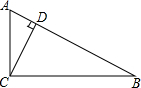 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于D