题目内容
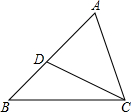 如图,△ABC中,D是AB上的一点,△ABC∽△ACD,且AD:AC=3:4,∠ADC=65°,∠B=43°.
如图,△ABC中,D是AB上的一点,△ABC∽△ACD,且AD:AC=3:4,∠ADC=65°,∠B=43°.(1)求∠ACB,∠ACD的度数;
(2)若AC=2,求AB的长.
考点:相似三角形的判定与性质
专题:
分析:(1)直接利用相似三角形的对应角相等这一性质即可解决问题.
(2)直接利用相似三角形的对应边成比例,列出比例式求解即可.
(2)直接利用相似三角形的对应边成比例,列出比例式求解即可.
解答: 解:(1)∵△ABC∽△ACD,
解:(1)∵△ABC∽△ACD,
∴∠ACB=∠ADC,∠ACD=∠B;
而∠ADC=65°,∠B=43°,
∴∠ACB=65°,∠ACD=43°.
(2)∵
=
,AC=2,
∴AD=
;
又∵△ABC∽△ACD,
∴
=
,AB=
=
=
,
即AB的长为
.
 解:(1)∵△ABC∽△ACD,
解:(1)∵△ABC∽△ACD,∴∠ACB=∠ADC,∠ACD=∠B;
而∠ADC=65°,∠B=43°,
∴∠ACB=65°,∠ACD=43°.
(2)∵
| AD |
| AC |
| 3 |
| 4 |
∴AD=
| 3 |
| 2 |
又∵△ABC∽△ACD,
∴
| AD |
| AC |
| AC |
| AB |
| AC2 |
| AD |
| 4 | ||
|
| 8 |
| 3 |
即AB的长为
| 8 |
| 3 |
点评:本题主要考查了相似三角形的性质及其应用问题;解题的关键是找准相似三角形的对应角和对应边,准确列出比例式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
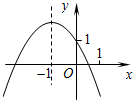 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论.其中,错误的结论是( )
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论.其中,错误的结论是( )| A、abc>0 | ||
| B、a+b<-1 | ||
C、2a-b<-
| ||
| D、c-a>1 |
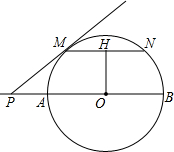 如图所示,AB是以O为圆心的半圆的直径,P在BA的延长线上,过P作半圆的切线PM,M是切点,弦MN∥AB,OH⊥MN,H为垂足,若OH=4,MN=6,求:
如图所示,AB是以O为圆心的半圆的直径,P在BA的延长线上,过P作半圆的切线PM,M是切点,弦MN∥AB,OH⊥MN,H为垂足,若OH=4,MN=6,求: 如图,已知AD平分∠BAC,要使△ABD≌△ACD,
如图,已知AD平分∠BAC,要使△ABD≌△ACD,