题目内容
已知在△ABC中，∠A=30°，BD是AC上的高，若
=
，求∠ABC．
| BD |
| CD |
| AD |
| BD |
考点：相似三角形的判定与性质
专题：
分析：根据已知条件可直接判断△ADB∽△BDC，进而找出角与角之间的关系即可解决问题．
解答：解：∵BD⊥AC，
∴∠A+∠ABD=90°，∠ADB=∠BDC=90°；
又∵
=
，
∴△ADB∽△BDC，
∴∠CBD=∠A=30°；
∴∠ABC=∠ABD+∠CBD=90°，
即∠ABC=90°．
∴∠A+∠ABD=90°，∠ADB=∠BDC=90°；
又∵
| BD |
| CD |
| AD |
| BD |
∴△ADB∽△BDC，
∴∠CBD=∠A=30°；
∴∠ABC=∠ABD+∠CBD=90°，
即∠ABC=90°．
点评：考查了相似三角形的判定及其应用问题；解题的关键是找准图形中的对应元素，灵活运用相似三角形的判定及其性质解题．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
如图，AM、AN分别切⊙O于M、N两点，点B在⊙O上，且∠MBN=60°，则∠A的度数是（ ）| A、60° | B、70° |
| C、80° | D、140° |
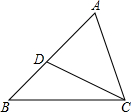如图，△ABC中，D是AB上的一点，△ABC∽△ACD，且AD：AC=3：4，∠ADC=65°，∠B=43°．
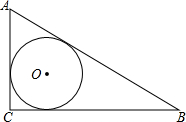如图，Rt△ABC中，∠C=90°，AB，BC，CA的长分别为c，a，b．求△ABC的内切圆半径r．