题目内容
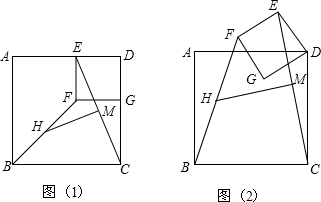
1. 已知:如图,在△ABC中,∠BAC=90°,AH⊥BC于H,以AB和AC为边在Rt△ABC外作等边△ABD和△ACE,求证:DH⊥HE.
已知:如图,在△ABC中,∠BAC=90°,AH⊥BC于H,以AB和AC为边在Rt△ABC外作等边△ABD和△ACE,求证:DH⊥HE.
分析 首先根据∠BAC=90°,AH⊥BC于H,判断出∠ABH=∠CAH,进而判断出∠DBH=∠EAH;然后根据相似三角形的判定方法,判断出△ABH∽△CAH,即可判断出$\frac{AB}{AC}=\frac{BH}{AH}$,再根据AB=BD,AH=AE,判断出$\frac{BD}{AE}=\frac{BH}{AH}$,据此判断出△BDH∽△AEH,推得∠BHD=∠AHE;最后判断出∠DHE=90°,即可判断出DH⊥HE.
解答 解:∵∠BAC=90°,
∴∠BAH+∠CAH=90°,
∵AH⊥BC,
∴∠ABH+∠BAH=90°,
∴∠ABH=∠CAH,
又∵∠DBH=∠ABH+60°,∠EAH=∠CAH+60°,
∴∠DBH=∠EAH,
在△ABH和△CAH中,
$\left\{\begin{array}{l}{∠ABH=∠CAH}\\{∠AHB=∠CHA}\end{array}\right.$,
∴△ABH∽△CAH,
∴$\frac{AB}{AC}=\frac{BH}{AH}$,
又∵AB=BD,AH=AE,
∴$\frac{BD}{AE}=\frac{BH}{AH}$,
在△BDH和△AEH中,
$\left\{\begin{array}{l}{\frac{BD}{AE}=\frac{BH}{AH}}\\{∠DBH=∠EAH}\end{array}\right.$
∴△BDH∽△AEH,
∴∠BHD=∠AHE,
∵∠BHD+AHD=90°,
∴∠AHE+AHD=90°,
即∠DHE=90°,
∴DH⊥HE.
点评 (1)此题主要考查了相似三角形的判定和性质的应用,要熟练掌握,解答此题的关键是要熟练掌握相似三角形的判定方法.
(2)此题还考查了等边三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:①等边三角形的内角都相等,且为60度;②等边三角形每条边上的中线、高线和所对角的平分线互相重合.③等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高或所对角的平分线所在的直线.

 优百分课时互动系列答案
优百分课时互动系列答案| A. | (-x-y)(-x+y)=x2-y2 | B. | $\frac{1}{x}$-x=$\frac{1-x}{x}$ | C. | x2-4x+3=(x-2)2+1 | D. | x÷(x2+x)=$\frac{1}{x}$+1 |
| A. | 5a2+3a2=8a4 | B. | a3•a4=a12 | C. | (a+2b)2=a2+4b2 | D. | -$\root{3}{64}$=-4 |
| A. | 精确到百分位,有3个有效数字 | B. | 精确到百分位,有5个有效数字 | ||
| C. | 精确到百位,有3个有效数字 | D. | 精确到百位,有5个有效数字 |
| A. | 2x-2y=2(x-y) | B. | (x+y)2=x2+2xy+y2 | C. | (x+2y)(x-2y)=x2-2y2 | D. | x2-4x+5=(x-2)2+1 |
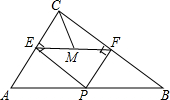 如图,已知在△ABC中,AC=3,BC=4,AB=5,点P是AB上 (不与A、B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E、F,连结EF,M为EF的中点.
如图,已知在△ABC中,AC=3,BC=4,AB=5,点P是AB上 (不与A、B重合),过P作PE⊥AC,PF⊥BC,垂足分别是E、F,连结EF,M为EF的中点.