题目内容
12.解下列不等式,井把解集在数轴上表示出来:(1)x+2<3-x;
(2)$\frac{x-3}{2}$<$\frac{2x+1}{3}$.
分析 (1)按照解不等式的基本步骤:移项、合并同类项、系数化为1可得不等式的解集,并表示在数轴上;
(2)按照解不等式的基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得不等式的解集,并表示在数轴上.
解答 解:(1)移项,得:x+x<3-2,
合并同类项,得:2x<1,
系数化为1,得:x<$\frac{1}{2}$,
不等式解集在数轴上表示如下:
(2)去分母,得:3(x-3)<2(2x+1),
去括号,得:3x-9<4x+2,
移项,得:3x-4x<2+9,
合并同类项,得:-x<11,
系数化为1,得:x>-11,
将不等式解集在数轴上表示如下:
点评 本题考查了解一元一次不等式得能力,正确解不等式,求出解集是解答本题的关键.

练习册系列答案
相关题目
2.关于反比例函数y=$\frac{5}{x}$,下列说法错误的是( )
| A. | 函数的图象不经过原点 | B. | 函数的图象一定在一、三象限 | ||
| C. | y的值随x值的增大而减小 | D. | 点($\frac{5}{2}$,2)在函数的图象上 |
3.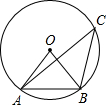 如图,A、B、C三点在⊙O上,∠C=30°,⊙O的半径长为3,则AB的长为( )
如图,A、B、C三点在⊙O上,∠C=30°,⊙O的半径长为3,则AB的长为( )
 如图,A、B、C三点在⊙O上,∠C=30°,⊙O的半径长为3,则AB的长为( )
如图,A、B、C三点在⊙O上,∠C=30°,⊙O的半径长为3,则AB的长为( )| A. | $\frac{3}{2}$ | B. | 3 | C. | 5 | D. | 6 |
7. 如图,⊙O的直径CD过弦EF的中点G,∠DCF=40°,则∠EOD等于( )
如图,⊙O的直径CD过弦EF的中点G,∠DCF=40°,则∠EOD等于( )
 如图,⊙O的直径CD过弦EF的中点G,∠DCF=40°,则∠EOD等于( )
如图,⊙O的直径CD过弦EF的中点G,∠DCF=40°,则∠EOD等于( )| A. | 10° | B. | 20° | C. | 40° | D. | 80° |
2.已知二次根式$\sqrt{x-1}$,x取下列各数会使二次根式无意义的是( )
| A. | $\sqrt{2}$ | B. | 1 | C. | 2 | D. | 0 |