题目内容
18. 如图,在△ABC中,DE∥BC,且AD=3,DB=2,AE=4,则EC=$\frac{8}{3}$.
如图,在△ABC中,DE∥BC,且AD=3,DB=2,AE=4,则EC=$\frac{8}{3}$.
分析 首先判定△AED∽△ACB,根据相似三角形的性质可得$\frac{AE}{AC}$=$\frac{AD}{AB}$,然后再代入数据可得答案.
解答 解:∵DE∥BC,
∴△AED∽△ACB,
∴$\frac{AE}{AC}$=$\frac{AD}{AB}$,
∵AD=3,DB=2,AE=4,
∴$\frac{4}{4+EC}$=$\frac{3}{5}$,
解得:EC=$\frac{8}{3}$,
故答案为:$\frac{8}{3}$.
点评 此题主要考查了平行线分线段成比例定理,关键是掌握平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列方程中,关于x的一元二次方程是( )
| A. | 3(x+1)3=2(x+1) | B. | x-1+5=0 | C. | ax2+bx+c=0 | D. | x2+2x=x-1 |
13.小强以5km/h的速度出发,16min后小明从同一地点出发,以13km/h的速度追赶小强,则小明从出发到追上小强所用的时间为( )
| A. | $\frac{1}{6}$h | B. | 10h | C. | $\frac{80}{13}$ | D. | 以上答案都不对 |
 如图,C岛在A岛的北偏东50o方向,C岛在B岛的北偏西40o方向,若AC=40海里,BC=20海里,则A,B两岛的距离等于20$\sqrt{5}$ 海里. (结果保留根号)
如图,C岛在A岛的北偏东50o方向,C岛在B岛的北偏西40o方向,若AC=40海里,BC=20海里,则A,B两岛的距离等于20$\sqrt{5}$ 海里. (结果保留根号) 的图象,当
的图象,当 时,
时, 随
随 的增大而减小,则
的增大而减小,则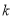 的取值范围是( )
的取值范围是( ) B.
B.  C.
C. 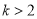 D.
D. 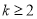

 ),若∠ABC的角平分线BD交AC于点D,且BD是△ABC的一条特异线,则∠BDC=______度;
),若∠ABC的角平分线BD交AC于点D,且BD是△ABC的一条特异线,则∠BDC=______度;