题目内容
1.从-1,0,π,3中随机任取一数,取到无理数的概率是( )| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
分析 由从-1,0,π,3中随机任取一数,无理数是π,直接利用概率公式求解即可求得答案.
解答 解:∵从-1,0,π,3中随机任取一数,无理数是π,
∴从-1,0,π,3中随机任取一数,取到无理数的概率是:$\frac{1}{4}$.
故选C.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
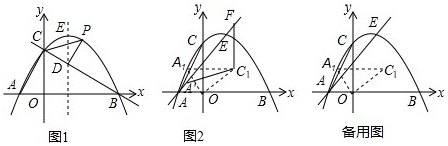
16. 如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于点F,则∠CFD的度数为( )
如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于点F,则∠CFD的度数为( )
 如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于点F,则∠CFD的度数为( )
如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于点F,则∠CFD的度数为( )| A. | 86° | B. | 76° | C. | 66° | D. | 52° |
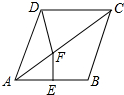
13. 如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )
如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )
 如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )
如图,点D在等边△ABC内,将△ABC绕点C顺时针旋转60°,得到△ACE,连接BE、DE,若∠AEB=45°,则∠DBE的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
11.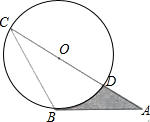 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是( )
如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是( )
 如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是( )
如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB=$\sqrt{3}$,则阴影部分的面积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{π}{6}$ | C. | $\frac{\sqrt{3}}{2}$-$\frac{π}{6}$ | D. | $\frac{\sqrt{3}}{3}$-$\frac{π}{6}$ |
 如下图所示,将长方形ABCD的一角折起来,使得B点和E点重合,而通过E点可以将AD边3等分.求FG的长度.
如下图所示,将长方形ABCD的一角折起来,使得B点和E点重合,而通过E点可以将AD边3等分.求FG的长度.
 如图,在直角坐标系中,已知点A(0,2),点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.
如图,在直角坐标系中,已知点A(0,2),点B(-2,0),过点B和线段OA的中点C作直线BC,以线段BC为边向上作正方形BCDE.