题目内容
16.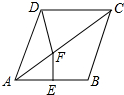 如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于点F,则∠CFD的度数为( )
如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于点F,则∠CFD的度数为( )| A. | 86° | B. | 76° | C. | 66° | D. | 52° |
分析 首先连接BF,易证得△ABF≌△ADF,继而可得∠CFD=∠CFB,由菱形ABCD中,∠BAD=76°,可求得∠BAC的度数,又由AB的垂直平分线EF交AC于点F,求得∠ABF=∠BAC=38°,继而求得答案.
解答  解:连接BF,
解:连接BF,
∵菱形ABCD中,∠BAD=76°,
∴∠BAC=∠DAC=$\frac{1}{2}$∠BAD=38°,AB=AD,
在△ABF和△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAF=∠DAF}\\{AF=AF}\end{array}\right.$,
∴△ABF≌△ADF(SAS),
∴∠AFD=∠AFB,
∴∠CFD=∠CFB,
∵AB的垂直平分线EF交AC于点F,
∴AF=BF,
∴∠ABF=∠BAC=38°,
∴∠CFB=∠BAC+∠ABF=76°,
∴∠CFD=76°.
故选B.
点评 此题考查了菱形的性质以及线段垂直平分线的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
7.一件工艺品的进价为100元,标价135元出售,每天可售出100件,根据销售统计,一件工艺品每降价1元,则每天可多售出4件,要使每天获得的利润最大,则每件需降价( )
| A. | 3.6 元 | B. | 5 元 | C. | 10 元 | D. | 12 元 |
4.已知二次函数y=x2-2x-3,点P在该函数的图象上,点P到x轴、y轴的距离分别为d1、d2.设d=d1+d2,下列结论中:
①d没有最大值;
②d没有最小值;
③-1<x<3时,d随x的增大而增大;
④满足d=5的点P有四个.
其中正确结论的个数有( )
①d没有最大值;
②d没有最小值;
③-1<x<3时,d随x的增大而增大;
④满足d=5的点P有四个.
其中正确结论的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.从-1,0,π,3中随机任取一数,取到无理数的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
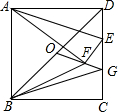 如图,在正方形ABCD中,AB=6,点E在边CD上,DE=$\frac{1}{3}$DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是$\frac{12}{5}$($\sqrt{5}$+$\sqrt{10}$).
如图,在正方形ABCD中,AB=6,点E在边CD上,DE=$\frac{1}{3}$DC,连接AE,将△ADE沿AE翻折,点D落在点F处,点O是对角线BD的中点,连接OF并延长OF交CD于点G,连接BF,BG,则△BFG的周长是$\frac{12}{5}$($\sqrt{5}$+$\sqrt{10}$). 已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.