题目内容
20.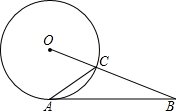 如图,⊙O与AB相切于点A,BO与⊙O交于点C,∠B=36°,则∠OCA=63度.
如图,⊙O与AB相切于点A,BO与⊙O交于点C,∠B=36°,则∠OCA=63度.
分析 连接OA;根据切线的性质和三角形内角和定理求解.
解答  解:连接OA.
解:连接OA.
∵⊙O与AB相切于点A,
∴∠OAB=90°.
∵∠B=36°,
∴∠AOB=180°-∠OAB-∠B=180°-90°-36°=54°.
∵OA=OC,
∴∠1=∠2=$\frac{1}{2}$(180°-∠AOB)=$\frac{1}{2}$(180°-54°)=63°.
故∠2=63°,即∠OCA=63°.
故答案为:63.
点评 此题主要考查切线的性质,三角形的内角和定理及等腰三角形的性质,连接OA,构造直角三角形是解题的关键.

练习册系列答案
相关题目
11.已知a2+Nab+64b2是一个完全平方式,则N等于( )
| A. | 8 | B. | ±8 | C. | ±16 | D. | ±32 |
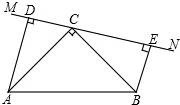 在△ABC中,∠ACB=90°,AC=BC,AD=8cm,BE=6cm,直线MN经过点C,且
在△ABC中,∠ACB=90°,AC=BC,AD=8cm,BE=6cm,直线MN经过点C,且