题目内容
5.化简$\sqrt{12}$=2$\sqrt{3}$,($\sqrt{3}$+$\sqrt{4}$)($\sqrt{3}$-$\sqrt{4}$)=1,($\sqrt{3}$$-\sqrt{4}$)2=7-6$\sqrt{3}$.分析 利用二次根式的性质化简$\sqrt{12}$,利用平方差公式计算($\sqrt{3}$+$\sqrt{4}$)($\sqrt{3}$-$\sqrt{4}$),利用完全平方公式计算($\sqrt{3}$$-\sqrt{4}$)2.
解答 解:$\sqrt{12}$=2$\sqrt{3}$,
($\sqrt{3}$+$\sqrt{4}$)($\sqrt{3}$-$\sqrt{4}$)=($\sqrt{3}$)2-($\sqrt{4}$)2=3-4=-1;
($\sqrt{3}$$-\sqrt{4}$)2=3-6$\sqrt{3}$+4=7-6$\sqrt{3}$.
故答案为2$\sqrt{3}$;1;7-6$\sqrt{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
13.若$\frac{m}{2}+1$与$\frac{2m-7}{3}$互为相反数,则m=( )
| A. | 2 | B. | -2 | C. | $\frac{8}{7}$ | D. | -$\frac{8}{7}$ |
14.下面去括号正确的是( )
| A. | 3(a-b)=3a-b | B. | a-(b-c)=a+b-c | C. | a+(b+c)=a+b+c | D. | -(a-2b)=-a-2b |
15.下列说法错误的是( )
| A. | 无理数的相反数还是无理数 | B. | 无理数都是无限小数 | ||
| C. | 正数、负数统称有理数 | D. | 实数与数轴上的点一一对应 |
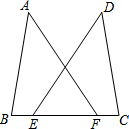 如图,点E、F在BC上,BE=CF,AB=DC,AF=DE.求证:∠B=∠C.
如图,点E、F在BC上,BE=CF,AB=DC,AF=DE.求证:∠B=∠C.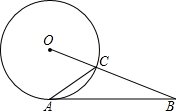 如图,⊙O与AB相切于点A,BO与⊙O交于点C,∠B=36°,则∠OCA=63度.
如图,⊙O与AB相切于点A,BO与⊙O交于点C,∠B=36°,则∠OCA=63度.