题目内容
14.已知点A、B的坐标分别为(-1,0)、B(3,0),点C在y轴正半轴上,且△ABC的面积为6.(1)求点C的坐标;
(2)以点A、B、C为顶点作?ABCD,写出点D的坐标.
分析 (1)审题可知点A和点B在x轴上,距离可用横坐标之差的绝对值求出,C点在Y轴上可设C(0,m) m>0,到x轴的距离是m,用面积列方程求解即可;
(2)根据平行四边形的性质对边平行且相等,分类求出点D的坐标即可.
解答 解:
(1)设点C(0,m)m>0,点A和点B在x轴上,可知点C到AB的距离是m,AB=3-(-1)=4,
由△ABC的面积为6,得$\frac{1}{2}$×4m=6,解得m=3,
所以:点C(0,3)
(2)如图:当CD∥AB时,CD=AB=4,由C(0,3)得D点坐标为(4,3)和(-4,3)
当BC∥AD时,过点D作DM垂直x轴,在平行四边形ABCD中,AC=BD,AC∥BD,
∴∠CAO=∠DBM,
又∵∠AOD=∠BMD=90°,
∴△AOC≌△BMD,
∴BM=AO=1,MD=OC=3,
OM=OB-BM=3-1=2,
∴点D的坐标为(2,-3),
综上所述:点D的坐标为(2,-3),(4,3),(-4,3).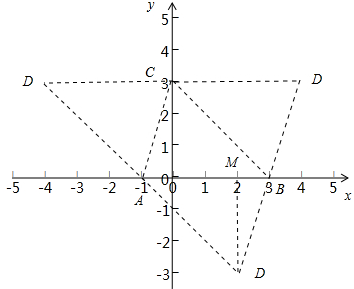
点评 此题主要考察坐标系中的坐标与图形,理清图形的性质,建立线段之间的关系,并熟悉用点的坐标表示线段是解题的关键.

练习册系列答案
相关题目
4.两个直角三角形全等的条件是( )
| A. | 一个锐角对应相等 | B. | 一条边对应相等 | ||
| C. | 两条直角边对应相等 | D. | 两个角对应相等 |
9.已知:分式$\frac{{x}^{2}+2x-3}{|x|-1}$的值为零,分式$\frac{{y}^{2}-3}{{y}^{2}+y-2}$无意义,则x+y的值是( )
| A. | -5或-2 | B. | -1或-4 | C. | 1或4 | D. | 5或2 |
6. 如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
 如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )| A. | AC=BC+CE | B. | ∠A=∠2 | C. | △ABC≌△CED | D. | ∠A与∠D互余 |
4.永登县明天降雪的概率是30%,对此消息下列说法中中正确的是( )
| A. | 永登县明天将有30%的地区降雪 | B. | 永登县明天将有30%的时间降雪 | ||
| C. | 永登县明天降雪的可能性较小 | D. | 永登县明天肯定不降雪 |
 如图,一次函数y=-2x+4的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,求:
如图,一次函数y=-2x+4的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,求: