题目内容
4.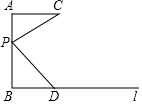 如图,线段AC和直线l分别垂直线段AB于点A,B.点P是线段AB上的一个动点,由A移动到B,连接CP,过点P作PD⊥CP交l于点D,设线段AP的长为x,BD的长为y,在下列图象中,能大致表示y与x之间函数关系的是( )
如图,线段AC和直线l分别垂直线段AB于点A,B.点P是线段AB上的一个动点,由A移动到B,连接CP,过点P作PD⊥CP交l于点D,设线段AP的长为x,BD的长为y,在下列图象中,能大致表示y与x之间函数关系的是( )| A. | 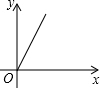 | B. | 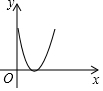 | C. | 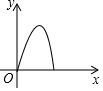 | D. | 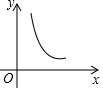 |
分析 根据相似三角形的判定和性质求得函数关系式,根据函数关系式即可得到结果.
解答 解:∵AC⊥AB,BD⊥AB,PD⊥CP,
∴∠A=∠B=∠CPD=90°,
∴∠C+∠APC=∠APC+∠BPD=90°,
∴∠C=∠BPD,
∴△ACP∽△BPD,
∴$\frac{AP}{BD}=\frac{AC}{PB}$,
设AC=a,AB=b,
则BP=b-x,
即$\frac{x}{y}$=$\frac{a}{b-x}$,
∴y=-$\frac{{x}^{2}}{a}$+$\frac{b}{a}$x,
∴y是x的二次函数,
故选C.
点评 本题考查了动点问题的函数图象,相似三角形的判定和性质,正确的求出函数关系式是解题的关键.

练习册系列答案
相关题目
14.在有理数-4,-2,0,3中,大小在-1和2之间的数是( )
| A. | -4 | B. | -2 | C. | 0 | D. | 3 |
15.G20峰会来了,在全民公益热潮中,杭州的志愿者们摩拳擦掌,想为世界展示一个美丽幸福文明的杭州.据统计,目前杭州注册志愿者已达9.06×105人,而这个数字还在不断在增加,请问近似数9.06×105的精确度是( )
| A. | 百分位 | B. | 个位 | C. | 千位 | D. | 十万位 |
9.小明有一块带秒针的手表,随意看一下手表,秒针在3时至4时(包括3时不包括4时)之间的可能性大小为( )
| A. | 1 | B. | $\frac{1}{60}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{12}$ |
16.分式$\frac{{x}^{2}-1}{x-1}$的值为0,则x的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
13.抛物线y=(x-1)2+t与x轴的两个交点之间的距离为4,则t的值是( )
| A. | -1 | B. | -2 | C. | -3 | D. | -4 |

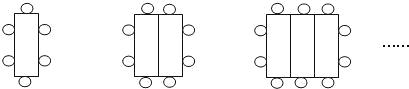
 如图,在平面直角坐标系中,点A是反比例函数y=$\frac{m}{x}$的图象上的一点,过点A作AB⊥x轴于点B,点C在y轴的负半轴上,连接AC,BC.若△ABC的面积为5,则m的值为( )
如图,在平面直角坐标系中,点A是反比例函数y=$\frac{m}{x}$的图象上的一点,过点A作AB⊥x轴于点B,点C在y轴的负半轴上,连接AC,BC.若△ABC的面积为5,则m的值为( )