题目内容
 要求tan30°的值,可构造如图所示的直角三角形进行计算:作Rt△ABC,使∠C=90°,斜边AB=2,直角边AC=1,那么BC=
要求tan30°的值,可构造如图所示的直角三角形进行计算:作Rt△ABC,使∠C=90°,斜边AB=2,直角边AC=1,那么BC= ,∠ABC=30°,tan30°=
,∠ABC=30°,tan30°= =
= =
= ,在此图的基础上通过添加适当的辅助线,可求出tan15°的值.请你写出添加辅助线的方法,并求出tan15°的值.
,在此图的基础上通过添加适当的辅助线,可求出tan15°的值.请你写出添加辅助线的方法,并求出tan15°的值.
解:两种方法(其他方法正确的都行)
(1)如图1.
延长CB到D,使BD=AB,连接AD,则∠D=15°.
tan15°= =
= =2-
=2- .
.

(2)如图2,延长CA到E,使CE=CB,连接BE.
则∠ABE=15°.
∵AE=CE-CA= -1,
-1,
∴AE= ,
,
∴BF=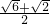 ,
,
∴tan15°= =2-
=2- .
.

分析:解答本题只要满足让15°角和已知的条件在一个直角三角形中即可.方法有很多,正确的都可以.
点评:本题其实是坡度坡角问题的一个变形,需掌握作辅助线构建直角三角形的方法.
(1)如图1.
延长CB到D,使BD=AB,连接AD,则∠D=15°.
tan15°=
 =
= =2-
=2- .
.
(2)如图2,延长CA到E,使CE=CB,连接BE.
则∠ABE=15°.
∵AE=CE-CA=
 -1,
-1,∴AE=
 ,
,∴BF=
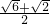 ,
,∴tan15°=
 =2-
=2- .
.
分析:解答本题只要满足让15°角和已知的条件在一个直角三角形中即可.方法有很多,正确的都可以.
点评:本题其实是坡度坡角问题的一个变形,需掌握作辅助线构建直角三角形的方法.

练习册系列答案
相关题目
 要求tan30°的值,可构造如图所示的直角三角形进行计算:作Rt△ABC,使∠C=90°,斜边AB=2,直角边AC=1,那么BC=
要求tan30°的值,可构造如图所示的直角三角形进行计算:作Rt△ABC,使∠C=90°,斜边AB=2,直角边AC=1,那么BC= ,∠ABC=" 30" °
,∠ABC=" 30" ° .
.
 ,∠ABC=30°,所以tan30°=
,∠ABC=30°,所以tan30°= ,在如图所示的基础上,通过添加适当的辅助线,可求tan15°的值,请简要写出你添加的辅助线,并求出tan15°的值。
,在如图所示的基础上,通过添加适当的辅助线,可求tan15°的值,请简要写出你添加的辅助线,并求出tan15°的值。 