题目内容
19.具有独特艺术风格的装饰性工艺品--厦门珠绣,已有一百多年的历史,因其新颖别致、富丽堂皇而备受青睐,某商场计划购进A,B两种珠绣汽车挂件.若购进A种挂件10件和B种挂件15件需4050元;若购进A种挂件5件和B种挂件10件需2400元.(1)求A,B两种挂件的进价分别是多少元?
(2)若购进A,B两种挂件共50件,总费用不超过8100元.
①最多能购进A种挂件多少件?
②若要求购买B种挂件的数量不超过A种挂件数量的$\frac{16}{9}$,有哪几种购进方案?
分析 (1)设A种挂件的进价是a元,B种挂件的进价是b元,根据题意列方程组即可得到结论.
(2)①设购进A种挂件x件,则购进B种挂件(50-x)件,根据题意列不等式即可得到结论.
②设购进A种挂件x件,则购进B种挂件(50-x)件,根据购买B种挂件的数量不超过A种挂件数量的$\frac{16}{9}$,可得购进方案.
解答 解:(1)设A种挂件的进价是a元,B种挂件的进价是b元,根据题意得:
$\left\{\begin{array}{l}{10a+15b=4050}\\{5a+10b=2400}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=180}\\{b=150}\end{array}\right.$.
答:A种挂件的进价是180元,B种挂件的进价是150元;
(2)①设购进A种挂件x件,则购进B种挂件(50-x)件,根据题意得:
180x+150(50-x)≤8100,
解得:x≤20,
∵x为整数,
∴x的最大整数解为20,
∴最多能购进A种挂件20件;
②设购进A种挂件x件,则购进B种挂件(50-x)件,根据题意得:
50-x≤$\frac{16}{9}$x,
解得x≥18,
∵x≤20,
∴18≤x≤20,
∴方案1:购进A种挂件18件,购进B种挂件32件;
方案2:购进A种挂件19件,购进B种挂件31件;
方案3:购进A种挂件20件,购进B种挂件30件.
点评 本题考查了二元一次方程组的应用,一元一次不等式的应用,解决问题的关键是读懂题意,找到关键描述语,找到所求的量的等量关系和不等关系.

练习册系列答案
相关题目
9.画出函数y=-2x+2的图象,结合图象回答下列问题:
(1)这个函数中,随着自变量x的增大,函数值y是增大还是减小?它的图象从左到右怎样变化?
(2)当x取何值时,y=0?
(3)当x取何值时,y>0?
(1)这个函数中,随着自变量x的增大,函数值y是增大还是减小?它的图象从左到右怎样变化?
(2)当x取何值时,y=0?
(3)当x取何值时,y>0?
4.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
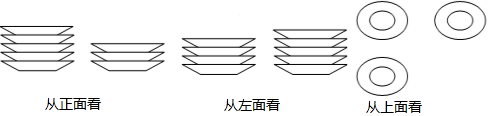
(2)分别从正面、左面、上面三个方向看这些碟子,看到的形状图如图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
| 碟子的个数 | 1 | 2 | 3 | 4 | … |
| 碟子的高度(单位:cm) | 2 | 2+1.5 | 2+3 | 2+4.5 | … |

(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从正面、左面、上面三个方向看这些碟子,看到的形状图如图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
8.钟表上的时间为9时30分,则时针与分针的夹角度数为( )
| A. | 90° | B. | 105° | C. | 120° | D. | 150° |
 如图,已知点A,B,C,D都在⊙O上,AC经过点O,且AC⊥BD,若∠ACB=50°,则∠ACD的度数为50°,∠BAD的度数为80°.
如图,已知点A,B,C,D都在⊙O上,AC经过点O,且AC⊥BD,若∠ACB=50°,则∠ACD的度数为50°,∠BAD的度数为80°. 如图:A、B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=2,且MN=4,P为直线上的动点,|PA-PB|的最大值为2$\sqrt{5}$.
如图:A、B两点在直线的两侧,点A到直线的距离AM=4,点B到直线的距离BN=2,且MN=4,P为直线上的动点,|PA-PB|的最大值为2$\sqrt{5}$. 在如图所示的平面直角坐标系中表示下面各点:A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7),G(5,0).
在如图所示的平面直角坐标系中表示下面各点:A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,7),G(5,0).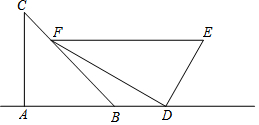 王生是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=4.求:
王生是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=4.求: